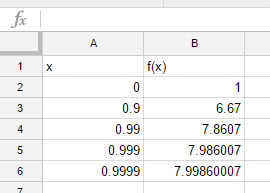
Suppose you want to generate a table of values from a formula…perhaps to help evaluate a limit. Google Sheets (or any spreadsheet) can quickly generate the values.
Category: Applied Calculus
Undo a Rate with the Substitution Method
Suppose that the profit for a company is increasing at a rate of
where the company has been in operation for t years. What is the total change in profit over the first three years?
Death and Piecewise Linear Functions
Although this may seem a little gruesome, it is not uncommon for businesses to give discounts for volume sales. In this case, a mortician charges less per pound for bodies weighing more than a certain amount.
The local mortician charges by the pound for embalming according to the following table:
Find a piecewise linear function that models the cost as a function of weight.
Rates and Rational Models
Many situations require us to take the derivative of a quotient. One situation like this is a model of a stocks price to earning ratio. In this situation the price is modeled by a function P(t) and the earnings by E(t).To find the rate at which the PE ratio is changing, you need to need to take the derivative of the model for the PE ratio.
The ratio is modeled by a quotient, P(t)/E(t). Since this is a quotient, we need to apply the quotient rule for derivative, 
but apply this to our functions. This means u will be replaced with P and v will be replaced with E to give
How Do You Find The Equation Of A Tangent Line?
A tangent line to a function is a line that looks most like the function at a point. In common terms, it just grazes the function.
To find its equation, we need to locate the point where the two meet as well as the slope of the function at that point. Then we can use the slope-intercept form or point-slope form of a line to get the equation.
Find the equation of the tangent line to
at x = 3.
Since this problem is asking for the equation of a line, let’s start with the point-slope form
This requires a point (x1, y1) and slope m. We’ll use the function to get the point and the derivative to get the slope of the tangent line.
Find the point: We are given a point x = 3. To find the corresponding y value, put the x value into the function
Find the slope of the tangent line: We need h′(3) to get the slope of the tangent line. We’ll use the Power Rule to take the derivative,
The slope of the tangent is
Write the equation of the tangent line: Putting the point (3, 10) and the slope 9 into the line yields
If you are asked to write this in slope-intercept form, you’ll need to solve this for y to give
If you graph h(x) and the tangent line together, it should be obvious that your tangent line is correct (ie. tangent).