Continue reading “How Do I Use the Doubling Time to Find the Rate?”
Category: Exponential and Log Functions in Finance
How Do I Solve An Exponential Equation For Sales That Decrease Exponentially?

Problem Monthly sales of a Blue Ray player are approximately
where t is the number of months the Blue Ray player has been on the market.
a. Find the initial sales.
Solution The initial sales occur at t = 0. The corresponding sales are
or 250,000 units.
b. In how many months will sales reach 500,000 units?
Solution Set S(t) equal to 500 and solve for t.
c. Will sales ever reach 1000 thousand units?
Solution Follow steps similar to part b.
Since the logarithm of zero is not defined, sales will never be 1000 thousand units.
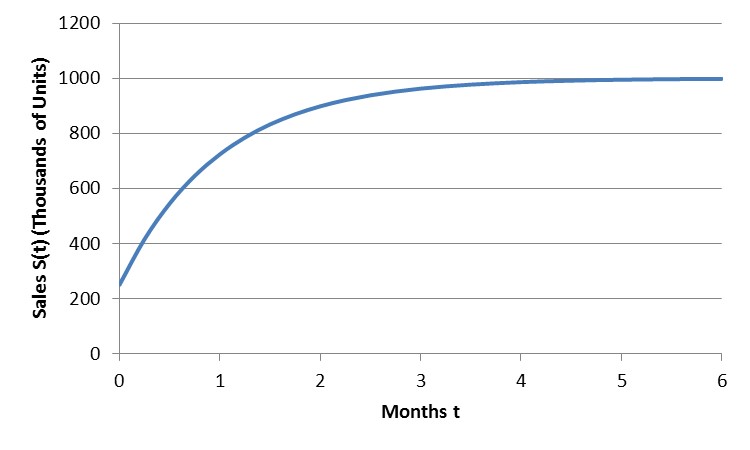
d. Is there a limit for sales?
Solution To help us answer this question, let’s look at a graph of S(t).
Examining the graph, it appears that the sales are getting closer and closer to 1000 units, but never quite get there (part c). So the limit for sales is 1000 thousand units or 1,000,000 units. This is due to the fact that as t increases, e–t gets smaller and smaller so all that is left from S(t) is 1000.