
Problem Assume the growth of the population of Del Webb’s Sun City Hilton Head community was linear from 1996 to 2000, with a population of 198 in 1996 and a rate of growth of 705 people per year.
a. Write an equation for the population P of the community where x is the number of years after 1990.
Solution The population of 198 in 1996 corresponds to the point (6, 198) since the variable x corresponds to years after 1990. We’ll write the slope-intercept form of the line, P = mx + b, and substitute m into the equation. The rate of growth, 705 people per year, is the slope of the function. Therefore, the line describing the population is
P = 705x + b
To find the value of b, we need to substitute x = 6 and P = 198:
198 = 705(6) + b
-4032 = b
This gives us the equation,
P = 705x – 4032
b. Use the function to estimate the population in 2002.
Solution The year 2002 corresponds to x = 12. Substitute this value into the function to yield
P = 705(12) – 4032 = 4428
The population in 2002 will be 4428 people.
c. In what year will the population reach 10,000?
Solution In this part, set P = 10,000 and solve for x.
10000 = 705x – 4032
14032 = 705x
14032/705 = x
19.9 ≈ x
This corresponds to 1990 + 19.9 = 2009.9. So in the year 2009, the population will reach 10000. Since we are asking in what year, we DO NOT round up on the answer.

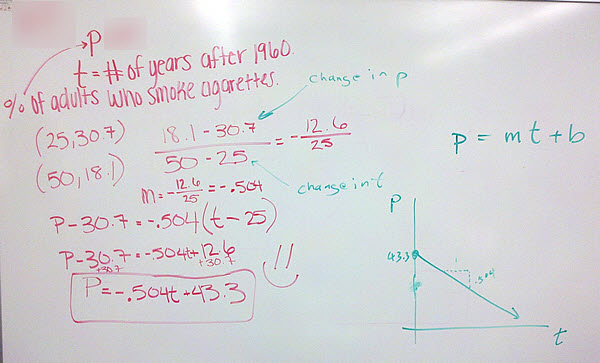


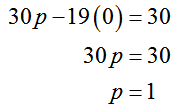

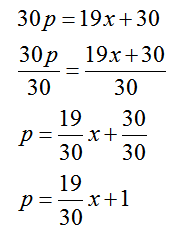
 In an earlier FAQ, we
In an earlier FAQ, we 



