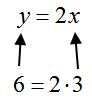What are independent and dependent variables?
A variable is a symbol that represents a quantity that may vary. Typically a variable is a letter of the alphabet. However, not all letters of the alphabet are necessarily variables. For instance, in physics the letter c is a constant that represents the speed of light. It is called a constant because the speed of light in a vacuum does not change. Letters in other alphabets such as the Greek alphabet can also be variables or constants. The letter π (pronounced pi) is a constant used in geometry that has a value that is approximately 3.14157.
Mathematics allows us to describe relationships between quantities in a variety of ways. In your mathematical experience, you have probably been exposed to formulas that relate variables like x and y. There is nothing special about the letters x and y. We could have used any letters in a formula. However, most algebra classes use the variables x and y so we’ll start there and introduce other variables later that are appropriate in finite mathematics.
A very simple formula that relates the variables x and y is
Since this formula is solved for y, you might think of substituting a number in place of x to obtain a value for y. For instance, a value of x = 3 corresponds to a value of y = 6,
We think of this as inputting the value of x = 3 to obtain an output of y = 6. The variable corresponding to the input, x, is called the independent variable. The variable corresponding to the output, y, is the dependent variable. We use the term dependent to emphasize the fact that the value for y depends on the input x. There is nothing special about the letters used in the relationship or even which letter matches with the independent or dependent variables. These terms are used to help describe the input and output from a relationship between two variables. Consider the formula
Since this formula is solved for x, we would use it to take a value for y to compute a value for x. In this case we would think of y as the independent variable and x as the dependent variable. This means that an input of y = 6 corresponds to an output of x = 3. These are the exact same values as The reason for this is that
![]()
![]()
Whether we start with x and multiply by 2 to get y or start with y and divide by 2 to get x, the relationship between x and y is the same. The only change is our perspective on the independent and dependent variable. In each of these cases, the variable that is solved for is the dependent variable.
The picture gets murkier if the equation is not solved for a variable. Suppose we have the equation
This equation is not solve for x or y. It is not clear whether x or y is the independent variable. In a case like this, we can specify which variable is the independent variable. The choice we make may reflect the quantity the variable represents or may simply be our own personal choice.
If we decide to make the independent variable x, we need to solve the equation for y to yield
In this form, it is easy to input a value for x to calculate an output y. If we decide to make the independent variable y, we need to solve the equation for x to yield
If we have a value for y, this equation can be used to calculate an output x. The variable chosen for the independent variable is often up to the user. In other contexts the independent variable is determined by the traditional choice made by practitioners in the field.
Example 1 Write an Equation with a Specified Independent Variable
Suppose you have the equation ![]()
a. Write the demand equation with P as the independent variable.
Solution To write ![]()
If P is to be the independent variable, solve the equation for Q:
b. Write the demand equation with Q as the independent variable.
Solution If Q is to be the independent variable, solve the equation for P:
Economists traditionally choose the quantity Q to be the independent variable when working with demand functions. In this format, we can see that as the quantity Q demand by consumers increases, the price of the good must decrease to make it attractive to the consumer.