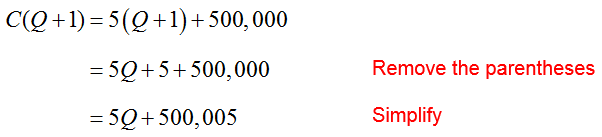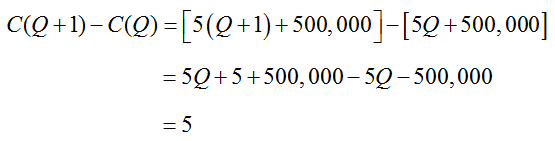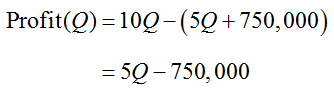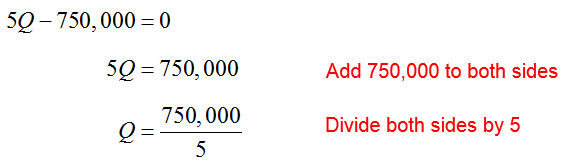What is function notation?
Problems in business and finance are often mathematical in nature. These problems come from real-world situations that can be extremely complex. A mathematical model is a mathematical representation of the situation. Often these representations take the form of functions.
For instance, businesses operate by obtaining money by the sales of goods and services. The amount of money obtained through the sales of goods and services is called revenue. Revenue is modeled by multiplying the quantity a good or service by the price of each unit of the good or service. We can write this model in mathematical form by writing
revenue = price per quantity × quantity
This representation allows the revenue to be calculated if the price and quantity are known. If we use letters to represent the quantities in the problem, we might write
R = P Q
where R is the revenue obtained from selling Q units of a good or service at a price of P per unit. As long as we know what each letter represents in the model, we can use it to calculate any one of the three quantities as long as we have the other two quantities.
In many problems involving revenue, the price is fixed at some value and we are interested in knowing how the revenue R changes as the quantity Q changes. In this case, we know that Q is the independent variable and P is a constant. Function notation helps us to indicate that Q is the independent variable. In function notation, a name is given to the function such as R. The name of the function is followed by a set of parentheses enclosing the independent variable.
By writing
R(Q) = P Q
we are indicating that Q is a variable and P is a constant.
The name of the function usually reflects the output or dependent variable in the problem. We could have just as easily written this function as
Revenue(Q) = P Q
This name emphasizes what the output from the function is.
Suppose we know that the price per unit for memory cards is fixed at $10 per unit. With this information, we can form the revenue function based on this price as
R(Q) = 10 Q
Using the function notation, we can specify the revenue at a specific quantity of memory cards by substituting a number in place of Q. If we want to know the revenue when a quantity of 200 memory cards is sold, we would write R(200). The expression R(300) indicates the revenue when 300 memory cards is sold. These values are calculated from the function by substituting the appropriate value of Q in the formula on the right side of the function’s definition:
R(200) = 10 (200) = 2000
R(300) = 10 ( 300) = 3000
We can also use function notation to indicate operation with functions. For instance, the expression R(300) – R(200) represents the difference in revenue between selling 300 memory cards and 200 memory cards.
Example 7 Revenue Function
Suppose the quantity of memory cards is fixed at 300 and we are interested in varying the price of each memory card to see its impact on revenue.
a. Use function notation to define revenue for this application as a function of the price P.
Solution We need to write a revenue function we’ll call R as a function of P, R(P). Using the model for revenue, we can set the quantity equal to 300 and define
R(P) = 300 P
To find the revenue from selling 300 memory cards at a price P, substitute the price into the function.
a. Use the function from part a to determine the increase in revenue from increasing the price of memory cards from $10 per card to $12 per card.
Solution To find the change in revenue, we need to calculate the difference between the revenue at a price of $12 per card and the revenue at a price of $10 per card. To find this difference, substitute 10 and 12 into the revenue function:
R(10) = 300 (10) = 3000
R(12) = 300 (12) = 3600
The difference is
R(12) – R(10) = 3600 – 3000 = 600
This means that increasing the price from $10 to $12 yields $600 in additional revenue.
In Example 7, the quantity Q of memory cards was fixed and the price P was variable. For this reason, the revenue function was denoted by R(P). In Example 8, we’ll apply function notation to a cost function.
Example 8 Cost Function
Suppose that the cost of memory cards is given by the function C(Q) = 5Q + 500,000 dollars where Q is the number of memory cards produced.
a. Find and interpret C(0).
Solution To find C(0), substitute Q = 0 into the right side of the function,
C(0) = 5 (0) + 500,000 = 500,000
This means that the cost of producing no memory cards is $500,000. These costs are called fixed costs and are incurred even though no cards are produced.
b. Find and interpret C(100) – C(99).
Solution We’ll start by evaluating the cost function at 99 memory cards and 100 memory cards:
C(99) = 5 (99) + 500,000 = 500,495
C(100) = 5 (100) + 500,000 = 500,500
The difference in these costs is found by subtracting the costs,
C(100) – C(99) = 500,500 – 500,495 = 5
The cost of producing 100 memory cards is $500,500 and the cost of producing 99 memory cards is $500,495. Thus the 100th memory card costs C(100) – C(99) or $5.
c. Find and interpret C(Q+1) – C(Q).
Solution If C(Q) = 5Q + 500,000, we can find C(Q+1) by replacing Q with Q + 1,
To find the difference in the costs at the two production levels, we’ll subtract the two formulas:
This means that the difference in costs between any two consecutive production levels Q and Q + 1 is $5.
The name of a function is arbitrary, but care needs to be taken so that names are not confusing. Quantities beginning with the letter p are especially problematic. Two different economic quantities begin with the letter p, price and profit. To distinguish between them, we’ll need to name them carefully.
Profit is the difference between revenue and cost. We can write this mathematically as
profit = revenue – cost
If the amount received from sales is greater than the cost, the profit is positive since the revenue is greater than the cost. On the other hand, if the costs are greater than the revenue, the profit is negative.
To name a profit function with an independent variable Q, we might want to write P(Q). Although this is perfectly acceptable, the name P might be confused with the variable P representing price. To avoid this confusion, it would be wise to use the name Profit(Q). This function takes the quantity Q of some good or service and outputs the profit at that production level.
If a word is used to name a function instead of simply a letter, we should probably continue this pattern with other related function. Instead of R(Q) for the revenue function, we could use the name Revenue(Q). Instead of C(Q) for the cost function, we could use the name Cost(Q). The names are very descriptive of exactly what the function does and allow us to write the relationship between these functions as
Profit(Q) = Revenue(Q) – Cost(Q)
The name of a function is up to the user. Some textbooks might choose to use an entire world while others might use a single letter. We’ll use both naming conventions so you get used to them.
Example 9 Profit Function
The cost of producing robotic hamsters at an Asian manufacturing plant is Cost(Q) = 5 Q+750,000 dollars where Q is the number of robotic hamsters. The revenue from selling the toys is Revenue(Q) = 10 Q.
a. Find the profit function.
Solution The profit function is formed by subtracting Cost(Q) from Revenue(Q),
b. Find the profit at a production level of 100,000 robotic hamsters.
Solution Substitute Q equal to 100,000 into the profit function, Profit(Q) = 5Q – 750,000, to yield
Profit(100,000) = 5 (100,000) – 750,000 = -250,000
Since the amount is negative, the manufacturing plant loses $250,000 at a production level of 100,000 robotic hamsters.
c. The manufacturing plant breaks even when production is increased to a level where the profit is equal to $0. Find the production level where the plant breaks even.
Solution In this part we know the profit and want to find the corresponding production level. Instead of substituting a value for Q in the function and computing the profit from (like in part b), we’ll set Profit(Q) = 0 and solve for Q:
To break even, the manufacturing plant must produce 750,000/5 or 150,000 robotic hamsters. At higher production levels, the plant makes money.