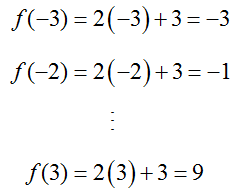What are the pieces of a linear function?
In section 1.1, we defined a linear function in the variables x and y,
y = mx + b
When the function is written this way, we say “y is a linear function of x”. This means the variable x is the independent variable and the variable y is the dependent variable. The other letters in this equation, m and b, correspond to numbers. For instance, in the equation y = 2x + 3 the value of the constant m is 2 and the value of b is 3. We distinguish between variables and constants since in any problem the constants will be given (or can easily be calculated) and the variables will vary as needed.
In every linear function of one independent variable, the right side of the function contains two terms. The first term, 2x, contains the constant m = 2 and the independent variable x. Since this term contains the variable, it is often called the variable term. As different values of x are put into the function, the product of the constant and the variable will change.
The second term 3 contains the constant b. Since this term never changes as values are put into the function, it is often called the fixed term.
In the case of y = 2x + 3, we can try values of x in the function and see how y depends on these values. Suppose we pick several values of x like x = -3, -2, … , 3. If we think of this equation as a function f (x) = 2x + 3, we can calculate the corresponding values of y:
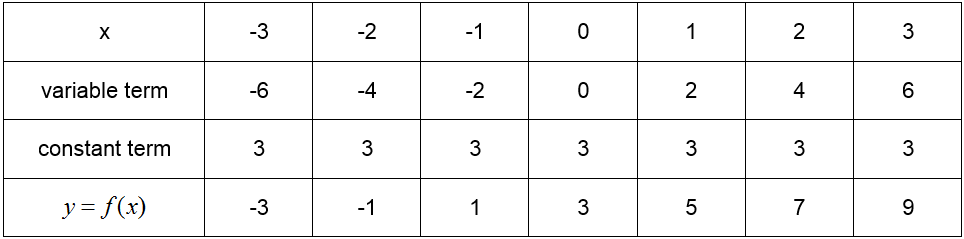
Let’s examine this behavior of the variable term and the constant term in a table.
Table 1
For each x value, the constant term does not change. However, as the x value increases by 1 unit, the variable term increases by 2 units. This increase is to the value of m, 2, multiplying the variable x. The y value in the last row is the sum of the variable and constant terms. Since the variable term increases by 2 units when the x value increases by 1 unit, so does the y value.