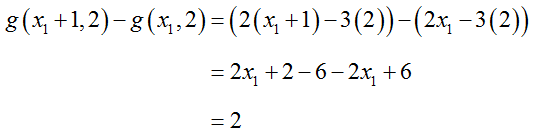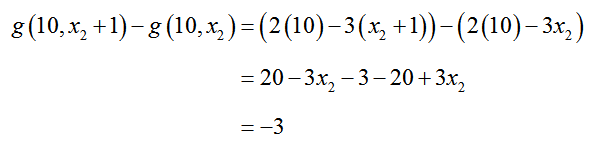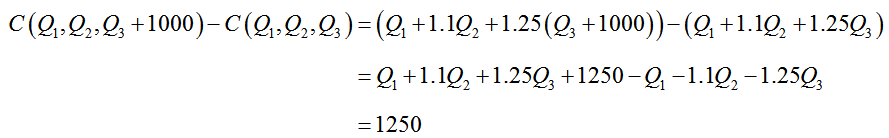What do the coefficients of the variables tell us?
For a linear function of one independent variable, the coefficient on the variable is the slope or rate of change. We can generalize this idea to linear functions of several variables. Let’s consider the function g (x1, x2) = 2x1 – 3x2. As we saw in Example 1, we can substitute values for the variables to obtain a value for the function. For instance, if we want to substitute 10 for x1 and 2 for x2 we get
g (10, 2) = 2(10) – 3(2) = 14
Now compare this value to the value obtained when we increase the value for x1 by 1 unit,
g (11, 2) = 2(11) – 3(2) = 16
The difference between these values is g (11, 2) – g (10, 2) = 16 – 14 = 2. Since the coefficient on is a 2, increasing the value for increases the value from g by 2 units. The coefficient on tells us the amount the function will change when increases by 1 unit.
In general, this applies for any value of x1. If we fix x2 at some value and find the difference between the function at x1 and at x1 + 1 we get
We can also apply this reasoning to the coefficient of x2. If we fix x1 at some value and find the difference between the function at x2 and x2 + 1 we get
The coefficient on x2, -3, indicates the amount the function will change when grows by 1 unit.
This leads to the following generalization.
If f (x1, x2,…, xn) = a0 + a1 x1 + a2 x2 + …+ an xn is a linear function of n independent variables, the coefficient for values of i from 1 to n indicates the amount the function will change when the variable is increased by one unit and all other variables are fixed.
Example 2 Interpret Coefficients
The function S(A, E) = 105A + 1412E describes the monthly sales, in thousands of dollars, at a large dairy distributor with E employees and A thousand dollars of monthly advertising costs.
a. What does the coefficient of E tell you about the monthly sales?
Solution The coefficient of E, 1412, relates the change in sales to the variable E when it is increased by 1 unit. An increase of 1 unit in E means an increase of 1 employee. This leads to an increase in sales of 1412 thousand dollars or $1,412,000.
b. What does the coefficient of A tell you about monthly sales?
Solution The coefficient of A, 105, relates the change in sales to the variable A when it increases by 1 unit. An increase of 1 unit in A means an increase of 1 thousand dollars in advertising. This leads to an increase in sales of 105 thousand dollars or $105,000.
We can now interpret what coefficients a1 through an mean, but what about the constant a0? The constant a0is similar to the vertical intercept b for a linear function of one independent variable . In that case, b is the value of the function when the variable is set equal to zero, f (0) = m(0) + b = b. For a linear function of n independent variables, the corresponding process is to set all independent variables equal to zero. If f (x1, x2,…, xn) = a0 + a1 x1 + a2 x2 + …+ an xn, we can set each variable equal to zero to obtain
f (0, 0,…, 0) = a0 + a1 (0) + a2 (0)+ …+ an (0) = a0
The only term that remains is the term containing the constant a0.
If f (x1, x2,…, xn) = a0 + a1 x1 + a2 x2 + …+ an xn, is a linear function of n independent variables, a0 is the value of the function when all independent variables are set equal to zero.
Example 3 Fixed Costs for an Organic Dairy
The daily cost function (in dollars) for an organic dairy is given by the linear function C(Q1, Q2, Q3) = Q1 + 1.1Q2 +1.25Q3 + 10,000 where is Q1 the number of gallons of whole milk produced, Q2 is the number of gallons of 2% milk produced, and Q3 is the number of gallons of 1% milk produced.
a. Find the fixed costs for the organic dairy based on this function.
Solution The fixed costs are costs incurred when nothing is produced. We can find this cost by finding C(0, 0, 0) or by noting that the constant gives the function’s value when all variables are zero. Either way, the fixed costs are $10,000.
b. How much does each additional gallon of 2% milk cost to produce?
Solution The coefficient of Q2 gives the change in the cost when Q2 is increased by 1 unit. In this case, the coefficient is 1.25 which tells us that another gallon of 2% milk will cost an additional $1.25.
We can calculate the amount it would cost to change production in Example 3 by any amount by adding the amount to the appropriate independent variable and utilizing the cost function. If we want to find the additional cost incurred from increasing the production of 1% milk by 1000 gallons, calculate
The extra 1000 gallons cost $1250. This number is independent of the initial production level. If we start with no 1% milk and increase production to 1000 gallons or increase production of 1% milk from 10,000 gallons to 11,000 gallons, the additional cost will be $1250. For linear functions like this one, the increase is always independent of the production level. Another way of thinking about this is that the variable costs for 1% milk are $1.25 per gallon. This is precisely the coefficient on the variable representing 1% milk, Q3.