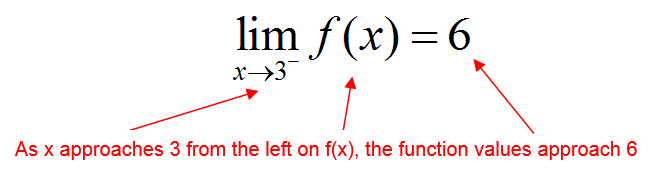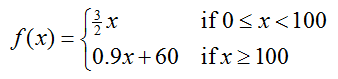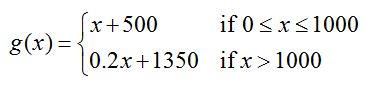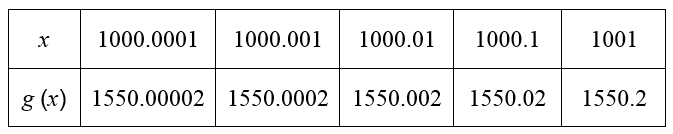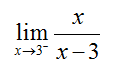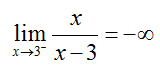How do you evaluate a limit from a table?
Suppose we have a rational function . We can examine the behavior of this function by constructing a table of values.
This function is undefined at x = 3 so we cannot find a function value there. However, we can find function values near x = 3.This table shows how the functions values change for different values of x near x = 3. In this table, x values on the left of 3 are in red. Values on the right side of 3 are in blue.
Let’s take a closer look at x values on the left side of x = 3.
On the left side of 3, the function values get closer and closer to 6 as x gets closer to 3. Mathematically, we say that the limit as x approaches 3 from the left is 6. A limit represents the relationship between x and f (x) as x approaches some value.
This relationship is represented symbolically using the symbol lim.
We read this as, “the limit of f (x) as x approaches 3 from the left is 6.” The value of the limit is determined by x values that are closer and closer to 3, not the value at x = 3. We will examine situations later in this section when we will use the value at a point to find the limit. In general, the value of the limit as x approaches some value is not equal to the value of the function at that x value. In the case of , the function is not even defined at x = 3.
A function f (x) has a limit L as x approaches a from the left, if the value of f (x) can be made arbitrarily close to L as x is made arbitrarily close to a from values on the left of a (but not equal to a). We symbolize this relationship by writing
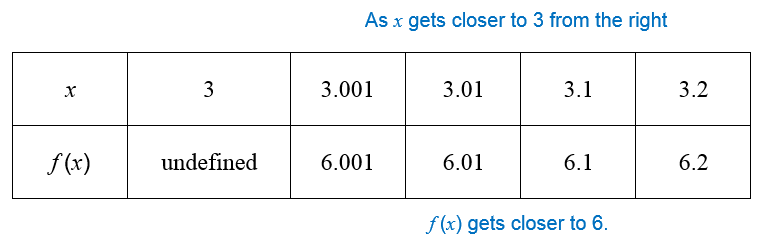
We can also evaluate a limit on the right side of on the function .
Based on this table, we see that as x gets closer and closer to 3 on the right, f (x) gets closer and closer to 6. This means that
The plus sign behind the x value indicates that we are approaching the value from the right side of 3. We read this as “the limit of f (x) as x approaches 3 from the right is 6.”
Example 1 Find a Limit Using a Table
Let f (x) be the piecewise function
Use a table to find each of the limits below.
Solution In this piecewise function, two expressions define the function. For x values in the interval [0, 100), the expression 3/2 x gives the y values for the function. We can use this expression to construct a table for values of x slightly to the left of x = 100.
As the x values in the table get closer and closer to 100, the corresponding f (x) values get closer and closer to 150. Based on this observation, we conclude that the left hand limit is
Solution For x values in the interval [100, ∞), the expression 0.9x + 60 gives the y values for the function. This expression can help us to form the following table of values slightly to the right of x = 100.
As x values get closer and closer to 100, the values for f (x) get closer and closer to 150. The right hand limit is
Solution Since the left hand and right hand limits are both equal to 150, the two-sided limit is also equal to 150,
Examples like the ones we have examined might lead you to believe that all limits are equal to some value. However, this is not always the case. In the next two examples, the limits do not exist.
Example 2 Find a Limit Using a Table
Let g(x) be the piecewise function
Use a table to find each of the limits below.
Solution In this limit, x is approaching 1000 from values on the left. On this side of 1000, the function is defined by the expression x + 500. Let’s examine the behavior of this expression slightly to the left of 1000.
As x approaches 1000, the values of get closer and closer to 1500. This indicates that the left hand limit is
Solution On the right hand side of 1000, the function is defined by the expression 0.2x + 1350. The table below shows values in that region.
Based on this table, as x approaches 1000 from the right, the function approaches 1550. Symbolically, we write
Solution In the previous parts, we evaluated the limits from the left and right. Since the limit from the left is not equal to the limit from the left, the two-sided limit does not exist.
Example 3 Find a Limit Using a Table
Use a table to evaluate the limit
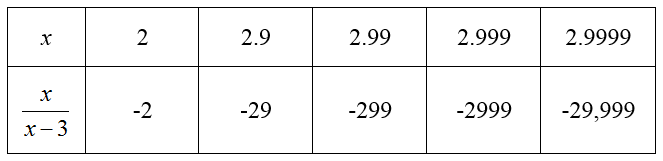
Solution Since this is a left hand limit, start by constructing a table of values slightly to the left of x = 3.
As x approaches 3, the value of the function gets more and more negative. Because the function is not approaching a value, we say that the limit does not exist.
Since it does the by growing large and negative, we write
For limits that do not exist and do it by becoming more and more positive, we write that the limit is equal to ∞. The infinity symbol always indicates that the limit does not exist because the values are becoming larger and larger.