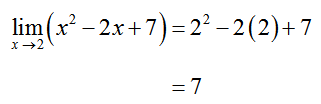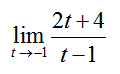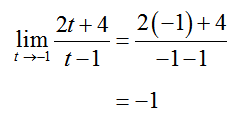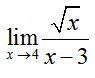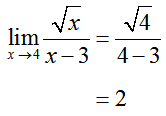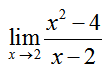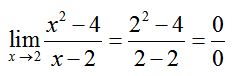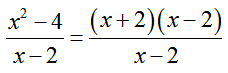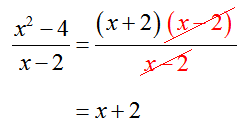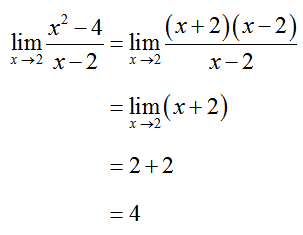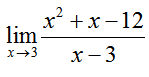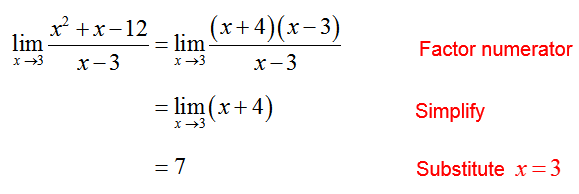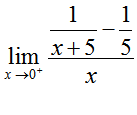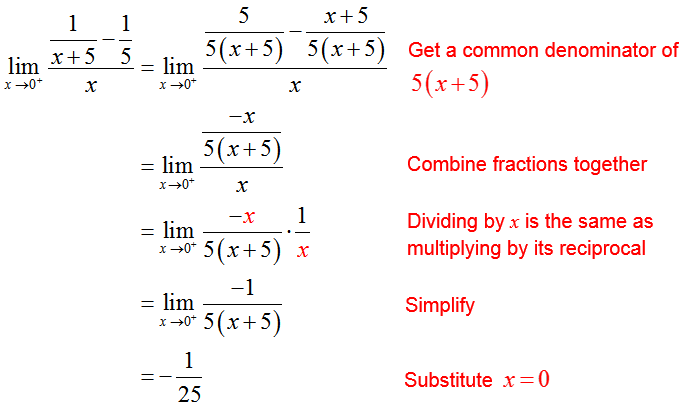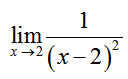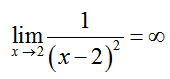How can a limit be computed algebraically?
For many functions, we can evaluate the limit by substituting the value the variable is approaching into the limit’s expression.
Basic Rule for Evaluating Limits Algebraically
If a function f (x) is made up of additions, subtractions, multiplications, divisions, powers and roots, then the limit as x approaches a may be evaluated by substituting x = a into the function f (x) as long as this function value is defined.
The basic rule applies to one and two sided limits.
Example 1 Evaluate the Limit
Evaluate each of the limits below.
Solution The polynomial is made up of additions, subtractions, powers, and multiplications so we may set x = 2 to find the limit:
Solution The rational expression is made up of additions, subtractions, multiplication and division so substitute t = -1 to find the limit:
Solution As with the earlier parts, substitute the value x is approaching to compute the limit:
Solution When we substitute x = 2 into the rational expression, the denominator is undefined. This means we need an alternate strategy for evaluating this limit.
The basic rule works in many cases. But limits like the one in part d of Example 1 require some extra steps. In this limit, substituting the value x is approaching in the limit results in
The numerator and denominator are both equal to zero. This occurs because the numerator contains a hidden factor of x – 2,
The factors of x – 2 in the numerator and denominator lead to the zeros in the numerator and denominator. Since these factors are the same, we can simplify the rational expression to yield
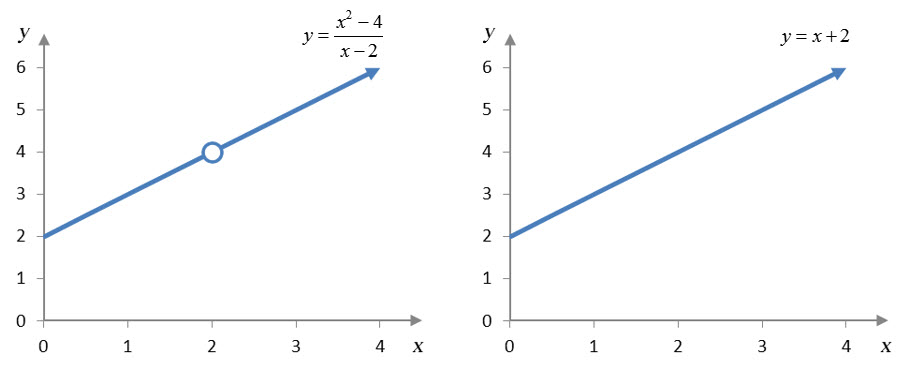
We have written and x + 2 as equal, but in what sense? Let’s examine the graph of each expression.
The graphs are identical except for the point at x = 2. The graph on the left is not defined at x = 2, but the graph on the right is defined there. This has no effect on the limit as x approaches 2. The y values on both functions get closer and closer to 4 as x approaches 2. This means we can simplify the rational expression and then substitute x = 2 into the result. This yields the limit
For limits that give 0/0 when the value is substituted, simplifying the expression often allows the limit to be evaluated by substitution.
Example 2 Evaluate the Limit
Evaluate each of the limits below.
Solution The numerator and denominator are both zero at x = 3. To evaluate the limit, simplify the expression before making the substitution:
Solution When you set x = 0, the numerator and denominator are both zero. To simplify the expression, combine the fractions in the numerator.
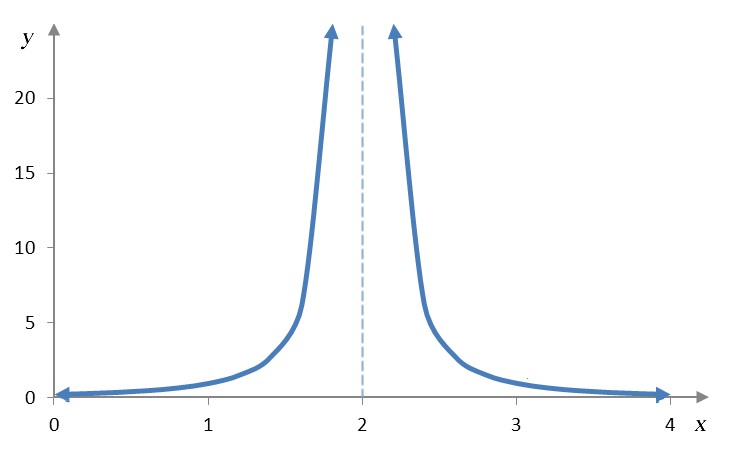
If the expression is undefined, but not because both the numerator and denominator are zero, we fall back to a table or graph to evaluate the limit. For example, in the limit
the denominator is zero when x = 2 is substituted. However, the numerator is not equal to zero. In this situation, a graph allows us to examine the behavior near x = 2.
As x gets closer and closer to 2 from the left or right, the y values grow larger and larger. In terms of the limit, we write
This means the limit does not exist since the y values grow larger and larger.