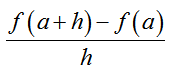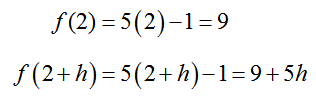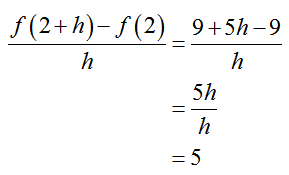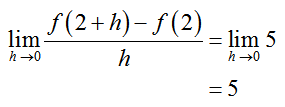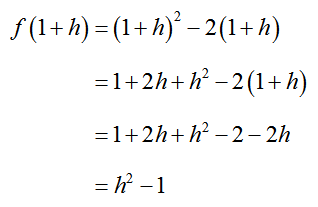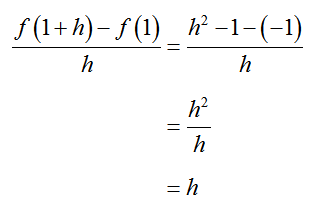How do you evaluate limits involving difference quotients?
In calculus, we frequently encounter expressions of the form
This type of expression is called a difference quotient. It may appear as part of a limit,
If we try to evaluate this limit by setting h = 0, both the numerator and denominator are zero. This indicates that we’ll need to try to simplify the difference quotient to evaluate the limit.
Example 3 Evaluate the Limit
Evaluate the limit
Solution Before attacking the limit, write out the difference quotient with the function and constant a. The two function values in the numerator are
With these values, we simplify the difference quotient:
With this simplification, the limit becomes
Since there is no h in the simplified difference quotient, setting has no effect on the constant. The limit of the constant is the equal to the constant.
As the function becomes more complicated, the algebra required to simplify the difference quotient may be more complicated. Pay careful attention to negative signs and removing parentheses.
Example 4 Evaluate the Limit
Evaluate the limit
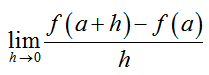
Solution The function value f (1) is easy to find,
However, the other function value requires several steps to simplify:
Put these values into the difference quotient and simplify to yield,
With the difference quotient simplified, we can evaluate the limit:
We’ll evaluate limits involving difference quotients in Chapter 11. The difficulty in evaluating the limits is not the concept of the limit itself. Instead, the algebra required to simplify the difference quotient is the most challenging aspect. It will require careful attention to algebra details.