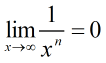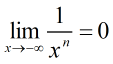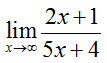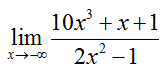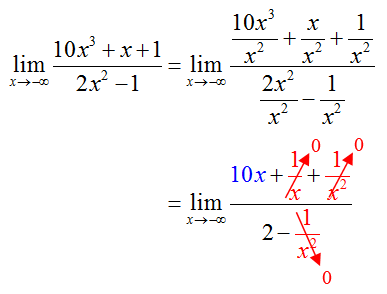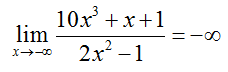How do you evaluate limits at infinity using algebra?
Limits involving rational expressions may be evaluated algebraically. To do this, we need to make an observation.
For any positive real number n,
or 
as long as xn is defined.
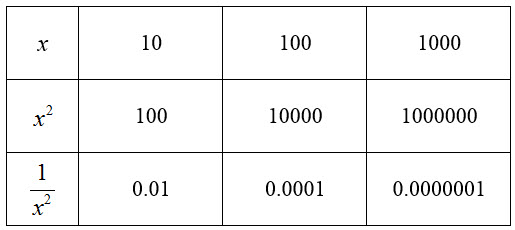
Consider the case where n = 2. A table of values for x2 and 1/x2 indicates how the parts of the rational expression behave.
As x grows larger in each limit, the denominator x2 also grows larger. This means the fraction 1/x2 grows smaller and smaller. When evaluating rational expressions, our goal is to simplify the terms in the expression so we can see which terms become smaller and smaller.
We need to be careful about these limits since the second limit is undefined for some values of n. For some values of n like n = 1/2, xn is undefined for negative x values since this amounts to taking an even root of a negative number. In these cases, the second limit as x approaches -∞ is not defined.
Example 4 Evaluate the Limit
Evaluate the limit algebraically: 
Solution Start by finding the highest power that appears on x in the denominator. The highest power on the variable in 5x + 4 is one. Divide each term in the fraction by x to this power to yield
For larger and larger values of x, the fractions 1/x and 4/x get smaller and smaller. As these terms approach zero, the constant terms are unchanged. The value of the limit is
The arrows help us to see how the individual pieces drop out as x gets larger.
Example 5 Evaluate the Limit
Evaluate the limit algebraically: 
Solution The highest power in the denominator is two. Divide each term in the rational expression by x2 and examine the resulting terms:
Each of the terms in red get small as x increases. This means the denominator approaches 1 but the numerator approaches 0.
Example 6 Evaluate the Limit
Evaluate the limit algebraically: 
Solution The highest power of the variable that appears in the denominator is two. Divide each term in the rational expression to give
Each of the terms in red grow smaller and smaller. However, the term in blue grows more and more negative as x grows more and more negative. If the numerator grows more and more negative, the fraction becomes more and more negative. The limit does not exist. Since it does this by becoming more and more negative, we write
