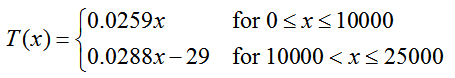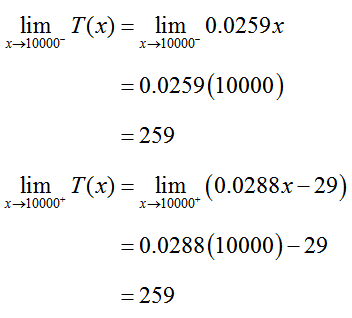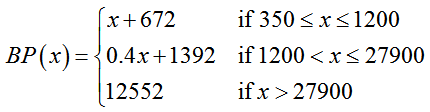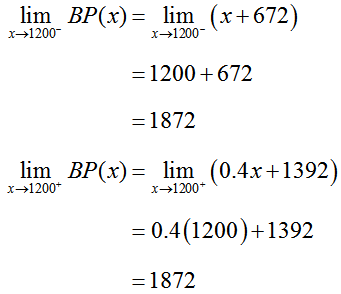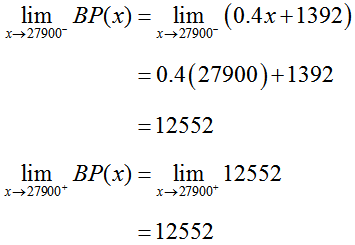How is a limit related to a continuous function?
The definition of continuity is related to limits.
Continuity at a Point
A function f is continuous at x = a if each of the conditions below are met.
1. f (a) is defined.
Let’s apply this definition to prove a function is continuous at some point. The state of Arizona uses a piecewise function to calculate the amount of tax T(x) in dollars. For taxable income from $0 to $25,000,
where x is the taxable income. Each piece of this function is a line and each line is continuous. However, do the two lines connect at x = 10000 or is there a discontinuity at that point?
To be continuous, all three conditions of the definition must be satisfied at x = 10000. Condition 1 requires that T(10,000) be defined. According to the function definition,
T(10000) = 0.0259(10000) = 259
This means that an individual with $10,000 in taxable income would pay $259 in tax. So the function is defined at x = 10000.
Condition 2 requires that the two sided limit exist at x = 10000. We will compute the one sided limits and make sure they exist.
The limit from the left and right are both equal to 259 so the two sided limit exists.
Condition 3 requires that the two sided limit be equal to T(10000). For Condition 2, we showed that
For Condition 1 we found that T(10000) = 259. This means that
The function is continuous at x = 10000.
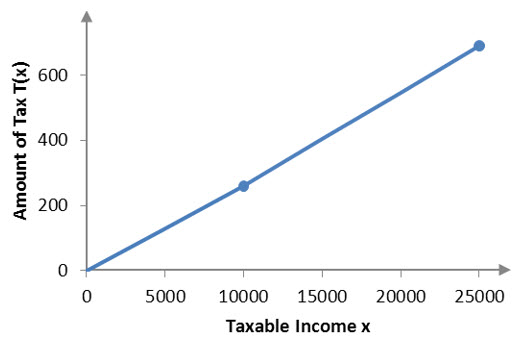
Figure 3 – The function T(x) is continuous at x = 10000.
As taxable income increases from the lower tax bracket to the higher tax bracket, the amount of tax paid increases continuously. This is due to the fact that the higher rate is only paid on income above 10,000. In effect, an individual in the higher tax bracket pays 2.59% on the first $10,000 in income and 2.88% on income above $10,000 up to $25,000. There is no big jump in the amount of tax paid.
Example 2 Continuous Function
The Basic Plus Plan is a medical insurance plan offered by a self insured trust in Northern Arizona. The total annual cost (in dollars) to an insured person is
where x is the amount of medical charges incurred at the point of treatment.
a. Prove that BP(x) is continuous at x = 1200.
Solution Check each condition in the definition of continuity at a point.
Condition 1:
BP(1200) = 1200 + 672 = 1872 is defined.
Condition 2:
The one side limits are equal so the two sided limit exists.
Condition 3: Since the one sided limits are both equal to 1872, the two sided limit is also equal to 1872. Additionally, BP(1200) = 1872. So
and the function is continuous at x = 1200.
b. Prove that BP(x) is continuous at x = 27900.
Solution Check each condition in the definition of continuity at a point.
Condition 1:
BP(27900) = 0.4(27900) + 1392 = 12552 is defined.
Condition 2:
The one side limits are equal so the two sided limit exists.
Condition 3: Since the one sided limits are both equal to 12552, the two sided limit is also equal to 12552. Additionally, BP(27900) = 12552. So
and the function is continuous at x = 27900.
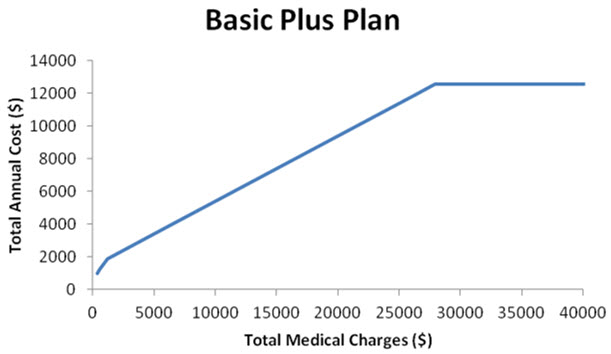
Each of the three pieces in Example 2 is continuous since they are each lines. Since the function is continuous at x = 1200 and x = 27900, the total annual cost increases continuously as the medical charges increase.
Figure 4 – The function BP(x) from Example 2.