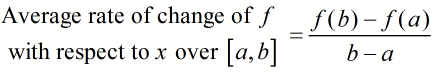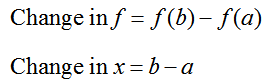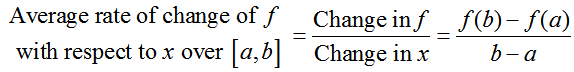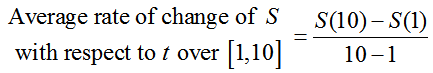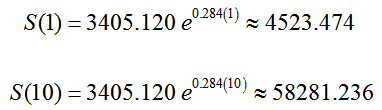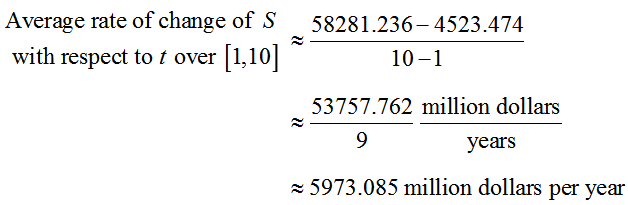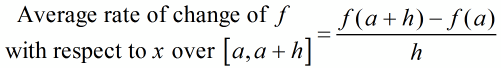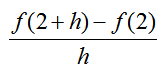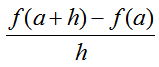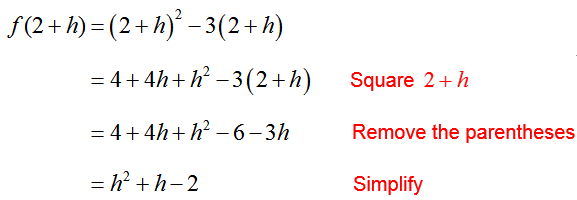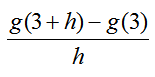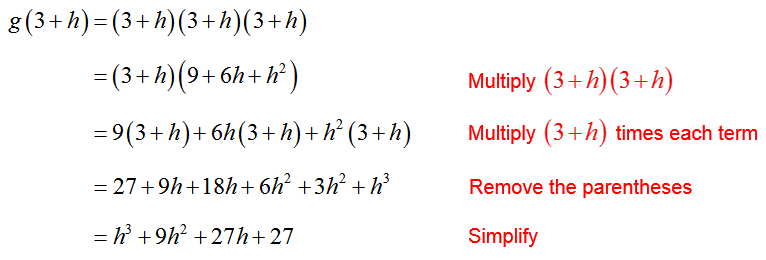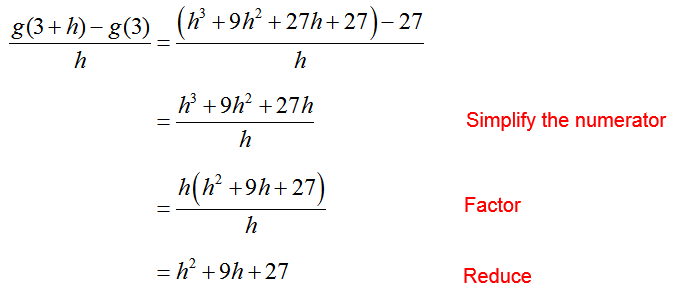How do you calculate the average rate of change from a function?
When a function is given by a formula, we modify the definition of average rate of change:
Average Rate of Change
The average rate of change of f (x) with respect to x from x = a to x = b is defined as
Close examination of this definition reveals that it is simply the same definition as before, but with
so that we can write
Instead of using the data values to calculate the changes in the difference quotient, we use the function’s formula to get the values in the numerator of the difference quotient.
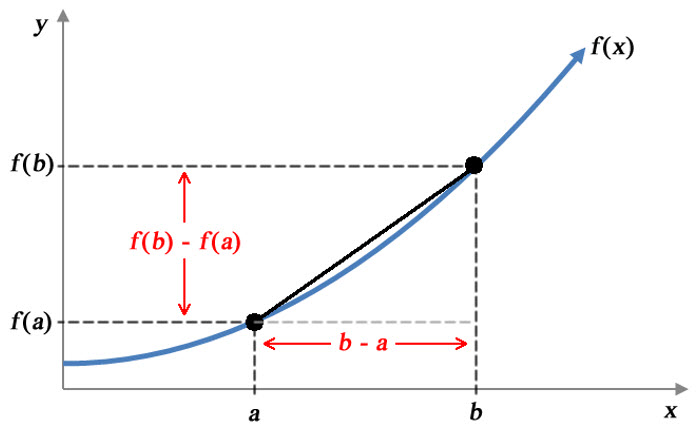
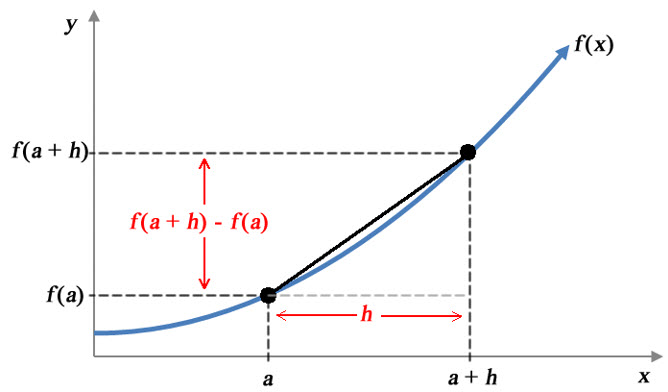
In the context of the graph of a function, the average rate of change of a function can be visualized as the slope of a line that passes through two points on the function. This line, called a secant line, can be drawn on a graph of a function so that we can quantify the value of the slope of the line.
Figure 1 – The average rate of change of f (x) with respect to x over [a, b] is equal to the slope of a line of a secant line.
A secant line passing through the points (a, f (a)) and (b, f (b)) has a vertical rise of f (b) – f (a) and a horizontal run of b – a. The slope of between the points on the secant line is
Example 4 Find the Average Rate of Change from a Function’s Formula
The annual sales (in millions of dollars) at Apple from 2001 through 2010 can be modeled by
where t is the number of years since 2000. Find the average rate of change of sales with respect to time over the period from 2001 to 2010.
(Modeled from Apple Annual Reports)
Solution Using the definition of the average rate of change,
The function values in the numerator are computed from the function’s formula,
This leads to the average rate of change,
Each decimal is written to three decimal places since the decimals in the original function were written to three decimal places. This average rate tells us that the sales increased by an average of about 5973.085 million dollars or $5,973,085,000 in each year from 2001 through 2010.
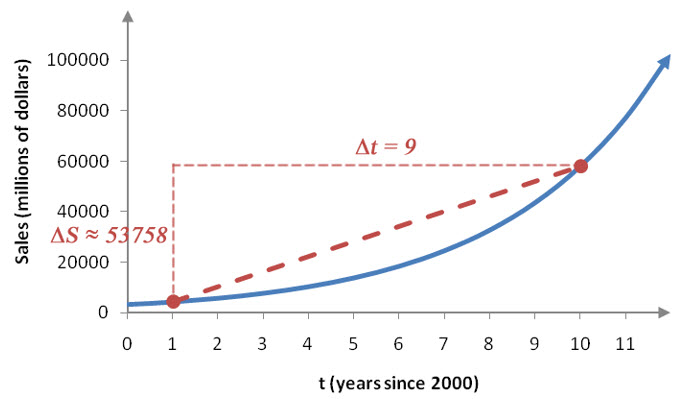
On a graph of the sales function S(t), the average rate of change of sales from t = 1 to t = 10 may be visualized as the slope of the line connecting the points at (1, S(1)) and (10, S(10)).
Figure 2 – The slope of the line connecting the sales at t = 1 and t = 10 is the same as the average rate of change between these points.
In calculus, one difference quotient in particular comes up very often.
This is the same definition we have been using with functions given by formulas, but with b = a + h. The value of h is the horizontal separation of the two points on the secant line. This difference quotient will be very important in defining the instantaneous rate of change in Section 11.2.
Example 5 Find the Difference Quotient
Let f (x)be defined by
a. Find and simplify the difference quotient
Solution This difference quotient is
with a = 2. Find the function values in the numerator of the difference quotient. The value f (2)is found by replacing x with 2 in the function,
Similarly, f (2 + h) is found by replacing x with 2 + h,
Substitute these function values into the difference quotient to yield
b. Evaluate the difference quotient in part a when h = 0.25.
Solution The expression for the difference quotient in part a, h + 1, makes it easy to evaluate the difference quotient for any value of h. It enables us to find the average rate of change of f (x) with respect to x from x = 2 and any other x value.
Set h = 0.25 to give
This value is the average rate of change of f (x) with respect to x from x = 2 to x = 2 + 0.25.
Care must be taken to calculate f (a + h) in the difference quotient. The most common mistake in simplifying the function value f (a + h) is to assume it is the sum of the values of the function. For instance, in the previous example f (2 + h) ≠ f (2) + f (h). The powers on the factors correspond to multiplication. They must be worked out when calculating f (a + h).
Example 6 Find the Difference Quotient
Find and simplify the difference quotient
for the function
Solution To find the difference quotient, we must evaluate g(t) at 3 and 3 + h. The value g(3) = 33 = 27 is easy to calculate. However g(3 + h) is more challenging:
To simplify the expression on the right, we need to cube the quantity 3 + h,
Now we can put the function values into the difference quotient and simplify: