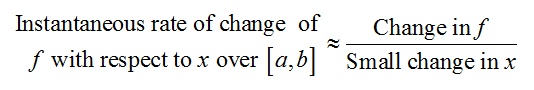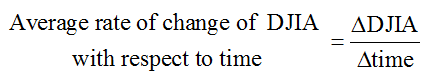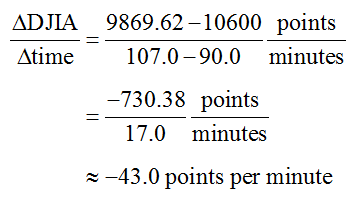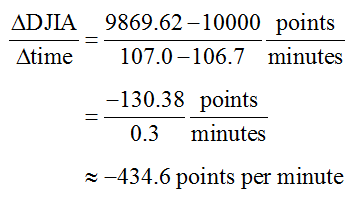How do you estimate the instantaneous rate of change?
The average rate of change of f with respect to x is computed using a difference quotient,
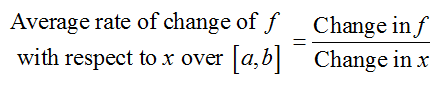
The smaller the change in the denominator, the better the estimate is of the instantaneous rate of change.
Example 1 Estimate the Instantaneous Rate of Change

At the time, this drop was the largest point drop during any day in history on the NYSE. Twenty minutes after dropping to a level of 9869.62 points, the index recovered around 600 points of the loss. This loss drove the NYSE to develop new trading curbs called “circuit breakers”. These circuit breakers dictate that trading will be halted on any stock on the S&P Index that changes by 10% in a five minute period.
Estimate the instantaneous rate of change of the DJIA 107.0 minutes after 1PM.
Solution The data in the table corresponds to the Dow Jones Industrial Average at various times after 1PM on May 6, 2010. The average rate of change over several different intervals is calculated using the definition of average rate of change,
For instance, the average rate of change of the Dow Jones Industrial Average over the interval [1.7, 107.0] is
An interval of length 105.3 minutes is certainly not an instant or even a reasonable approximation of an instant in time.
The average rate of change of the Dow Jones Industrial Average over the interval [90.0, 107.0] is
Even though the drop in points is not as steep as the previous interval, the average rate of change is greater since the interval is much shorter.
The average rate of change of the Dow Jones Industrial Average over the interval [103.3, 107.0] is
The endpoint on the right of the interval is fixed, but the left endpoint changes in each of these rates. To approximate an instant, we must make the endpoint on the left side of the interval as close as possible to t = 107.0.
The best approximation for the instantaneous rate of change is the average rate of change over the interval [106.7, 107.0],
For this table, an instant is approximated by an interval that is 0.3 minutes long and an instantaneous rate of change of -434.6 points per minute at the time immediately prior to when the Dow Jones Industrial Average began to rise again.
As the average rate of change is computed over smaller and smaller intervals near the lowest point on the graph, it gets more and more negative since the Dow Jones Industrial Average dropped faster and faster before recovering.