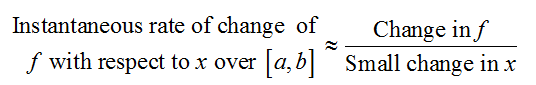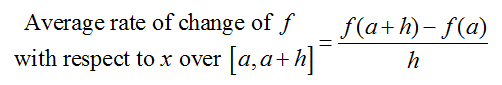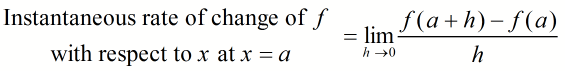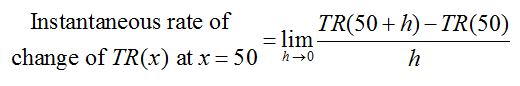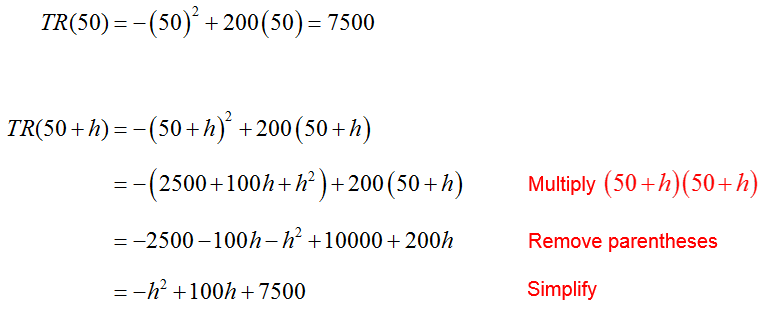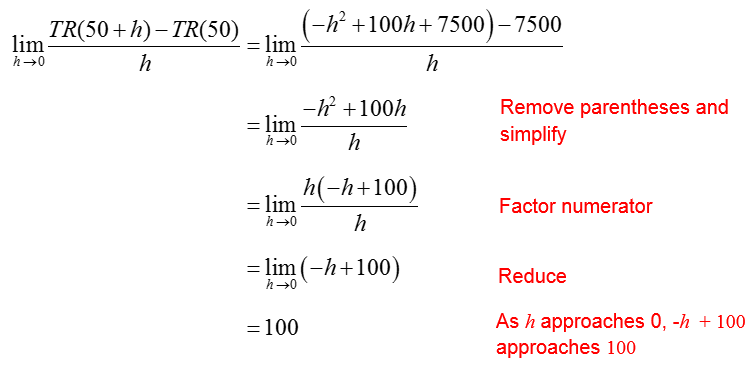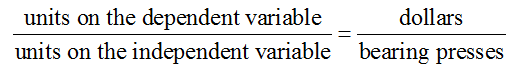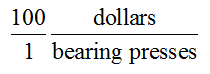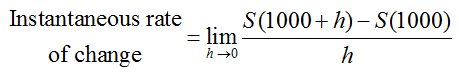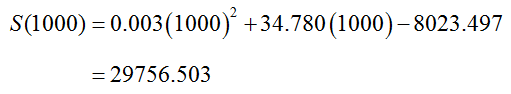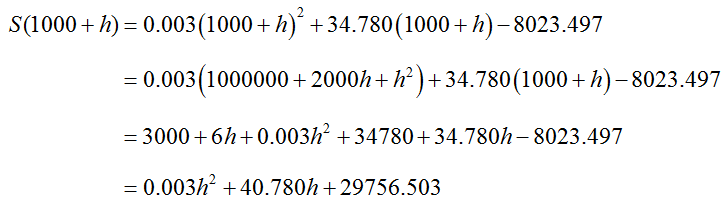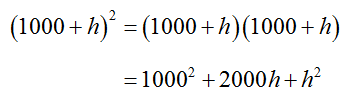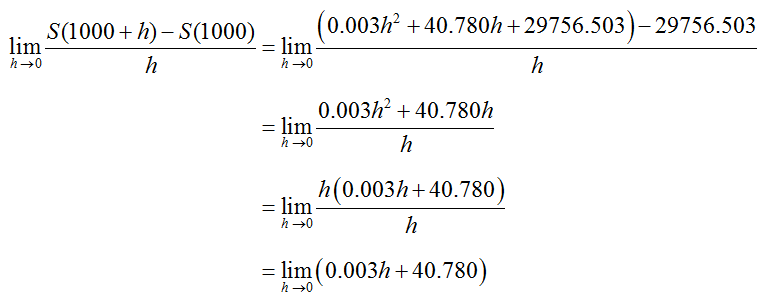How do you compute the instantaneous rate of change using a limit?
If the quantities being compared in an average rate of change are given by data, we can estimate the instantaneous rate of change using a difference quotient. By using the data nearest the point at which the instantaneous rate of change is desired, we calculate the difference quotient. In the case of the instantaneous rate of change of f with respect to x,
When the quantity in the numerator of the difference quotient is given by a formula, we do not have to settle for an estimate of the instantaneous rate of change. If the quantity in the numerator is given by a function f (x), we can write the average rate of change as
where h describes the magnitude of the change in the denominator. We can use this expression to write a corresponding definition for the instantaneous rate of change. For the instantaneous rate of change, we want the change h to be as small as possible. Although we cannot let this change be zero, we can do the next best thing using a limit.
By using a limit as the magnitude of the change h approaches zero, we are able to find the instantaneous rate of change by taking the limit of the average rate of change.
Example 2 Find the Instantaneous Rate of Change
A small toolmaker estimates the annual total revenue TR(x) from selling a quantity of x bearing presses to be
a. Find the instantaneous rate of change of annual total revenue with respect to the quantity of bearing presses sold when 50 bearing presses are sold annually.
Solution Start by rewriting the definition of instantaneous rate of change for the function TR(x) with a = 50,
To calculate the limit, we need to find the revenue function values in the numerator of the difference quotient:
These function values are substituted into the difference quotient to yield
b. Explain what the instantaneous rate of change in part a tells you about how revenue is changing as more bearing presses are sold.
Solution To help us understand what an instantaneous rate of change means in this context, let’s examine the units associated with this rate. For any rate, the units are the units on the dependent variable divided on the units on the independent variable. In this rate, the units on the dependent variable are dollars and the units on the independent variable are bearing presses. So the units on the rate are
An instantaneous rate of
means that selling one additional bearing press will increase revenue by 100 dollars.
Example 3 Find the Instantaneous Rate of Change
Apple is very successful in translating expenditures on research and development into sales of electronic products like Ipods, Iphones and Ipads. Based on data from 2001 through 2010, the annual sales at Apples (in millions of dollars) can be modeled by
where R is the amount, in millions of dollars, spent annually on research and development.
(Modeled from Apple Annual Reports)
a. Find the instantaneous rate of change of sales with respect to research and development spending when annual research and development spending is 1000 million dollars.
Solution For this function, the instantaneous rate of change of sales with respect to research and development spending when 1000 million dollars is spent on research and development is
We can find the function value S(1000) by substituting 1000 into the function,
The function value S(1000 + h) is found by replacing R with 1000 + h,
In simplifying this function value, take care to square the binomial 1000 + h properly. It is very common for students to write incorrectly
Instead, write the square as the product of two binomials and multiply the terms
Using the function values in the definition of instantaneous rate of change leads to
Note that only one term in the limit contains h. As h gets smaller, the term gets smaller and the constant term 40.780 does not change. We compute the limit to be
b. Explain what the instantaneous rate of change in part a tells you about sales and spending on research and development.
Solution The units on the variables help us to determine the units on the instantaneous rate. By dividing the units on the variables,
we get the units on the instantaneous rate of change. An instantaneous rate of 40.780 million dollars of sales per million dollars of research and development means that a one million dollar increase in research and development leads to an increase in sales of 40.780 million dollars. Alternately, we could also say that a one dollar increase in research and development leads to an increase in sales of 40.780 dollars since the factor of millions in the numerator and denominator of the units can be reduced.