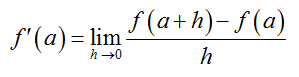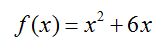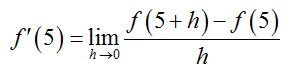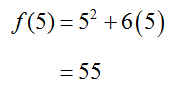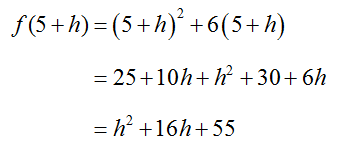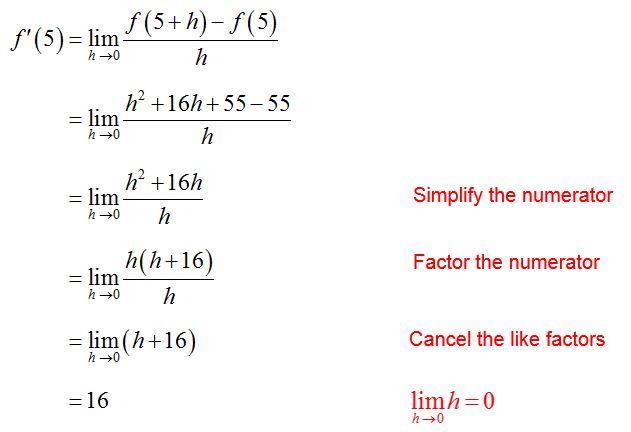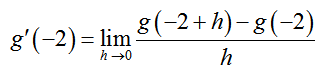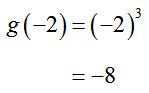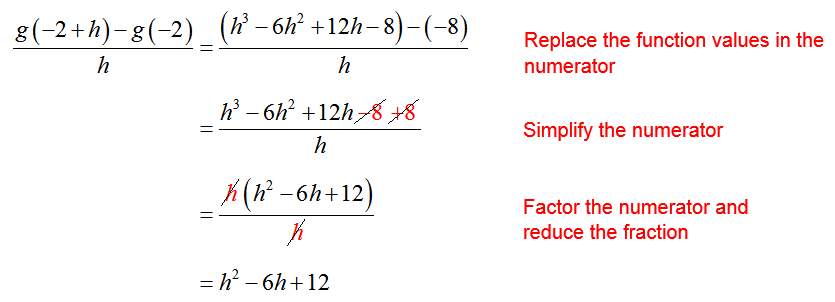Section 11.3 Question 2

How do you compute the derivative at a point using a limit?

In the previous question, we estimated the value of the derivative by estimating the slope of the tangent line on the graph of the function. If the function is given by a formula, we can find an exact value for the derivative at a point by applying the definition of the derivative directly. Recall that the derivative of a function y = f (x) at the point (a, f (a)) is defined by the limit

provided this limit exists. For many functions, we can find the value of the derivative by following several steps that help us to systematically evaluate the limit.

 

We’ll use this strategy to find the derivatives of several different functions evaluated at a point.

 Example 2    Compute the Derivative at a Point Using a Limit

Suppose the function f (x) is given by

Use the definition of the derivative at a point to compute f ′(5).

Solution The value of f ′(5) is found by evaluating the limit

The function values in the numerator are

and

Using these values in the definition of the derivative yields

The value of the derivative of f (x) at x = 5, f ′(5), is 16.

---

Example 3    Compute the Derivative at a Point Using a Limit

Suppose the function g (t) is given by

Use the definition of the derivative at a point to compute g′(-2).

Solution This function is named g(t) instead of f (x), so we need to modify the definition of the derivative of f (x) at a point x = a. Using g(t) in the definition and the point t = -2, we have

The function value g(-2) is calculated to be

The function value g(-2 + h) must be calculated carefully.

Form the difference quotient and simplify:

The derivative is completed by taking the limit as h approaches zero,

The derivative of g(t) evaluated at t = -2, g′(-2), is 12.