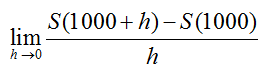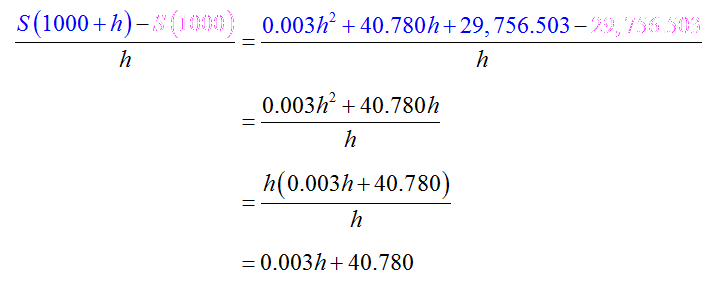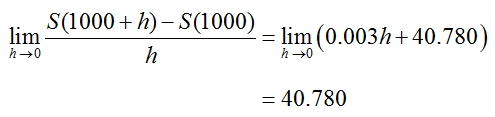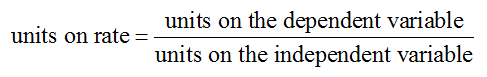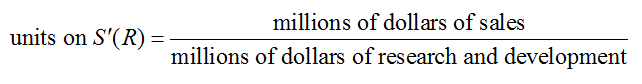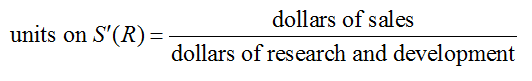Section 11.3 Question 4

What does the derivative at a point tell you about a function?

The derivative at a point is a rate so we may interpret it like any other rate of change. In general, we can use the units on the independent and dependent variable to find the units on the derivative.

Suppose a function is given by y = f (x) where x is the independent variable and y is the dependent variable. The units on the derivative of f (x) at x = a are

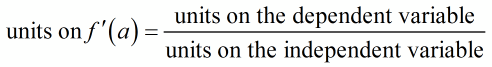
Once we have established the units on the derivative, we can use them to interpret what the derivative means.

Example 5    Find and Interpret the Derivative

Based on data from 2001 through 2010, the annual sales at Apple (in millions of dollars) can be modeled by

where R is the amount spent annually on research and development in millions of dollars.

a.   Find S′(1000).

Solution Using the definition of the derivative at a point, we must compute

We’ll do this by computing S(1000) and S(1000 + h). From these values and expressions we’ll form the difference quotient , simplify, and evaluate the limit.

Let’s look at the terms in the numerator of the difference quotient:

Now form the difference quotient and simplify:

The limit as h approaches 0 yields

The derivative is S′(1000) = 40.780.

b. What does the value you calculated in part a tell you about the relationship between sales and money spent on research and development?

Solution To interpret the derivative in part a, we need to establish the units on the derivative. A derivative has the same units as an average rate of change or an instantaneous rate of change for the function S(R),

In the case of the derivative S′(R), the units are

Notice that the numerator and denominator both are in millions of dollars. To distinguish the dollars of sales from the dollars of research and development, labels indicating the origin of the money are included.

The factor of millions in the numerator and denominator may be divided out to yield

The statement S′(1000) = 40.780 means that at a level of 1000 million dollars of research and development, sales are increasing at a rate of 40.78 dollars of sales per dollar of research and development. In other words, if research and development is increased by 1 dollar at this point, sales will increase by approximately 40.78 dollars.