What is the difference between a relative extremum and an absolute extremum?
The high and low points on a graph are called the extrema of the function. An extremum that is higher or lower than any other points nearby is called a relative extremum. A relative extremum (the plural of extremum is extrema) that is higher than points nearby is called relative maximum. A relative extremum that is lower than points nearby is called a relative minimum.
The point (c, f (c)) is a relative maximum of a function f if there exists an open interval (a, b) in the domain of f containing c such that f (x) ≤ f (c) for all x in (a, b).
The point (c, f (c)) is a relative minimum of a function f if there exists an open interval (a, b) in the domain of f containing c such that f (x) ≥ f (c) for all x in (a, b).
According to this definition, a relative extremum may not occur at the endpoint of an interval. Keep in mind that some textbooks define a relative extremum so that it may occur at the endpoints. The definition above is quite simple and will suffice for most business applications.
Example 1 Find the Relative Extrema
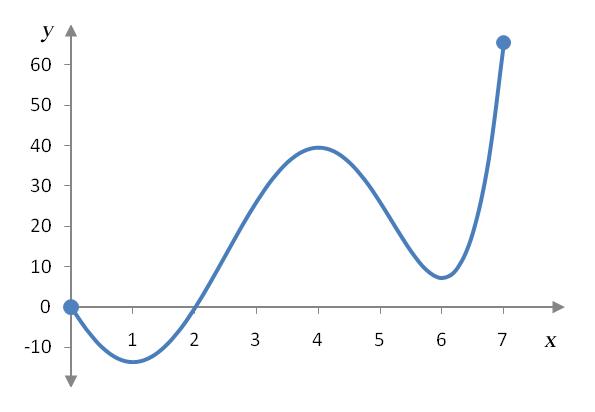
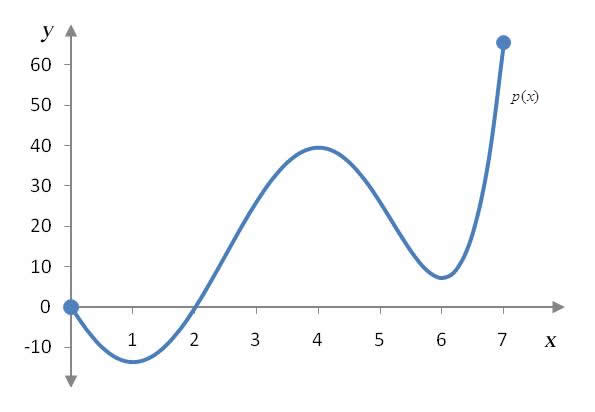
The function p(x) is defined on the interval [0, 7] in the graph below. Find all relative extrema of p(x).
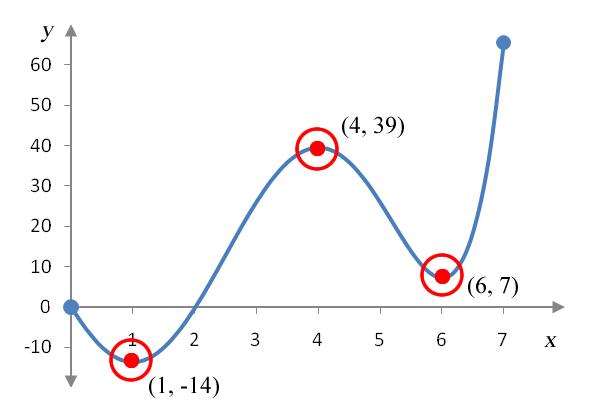
Solution The relative extrema are the highest and lowest points on the graph compared to the points nearby. We can check this by drawing a small circle around each potential relative extrema to illustrate the open interval.
For x values in the small circles, the points (1, -14) and (6, 7) are lower than any other points in the immediate neighborhood and are relative minima. The point (4, 39) is higher than any other points in the neighborhood of points indicated by the circle. This makes (4, 39) a relative maximum.
Example 2 Find the Relative Extrema
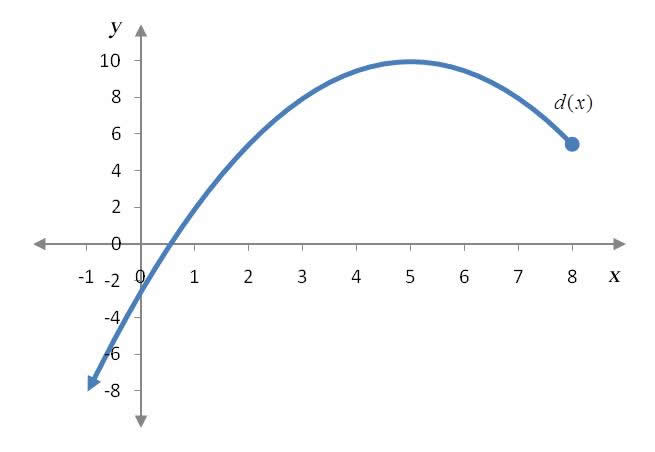
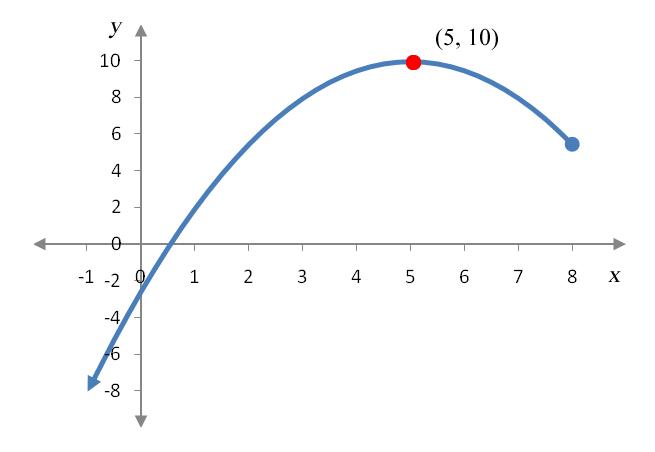
The function d(x) is defined on the interval (-∞, 8] in the graph below. Find all relative extrema of d(x).
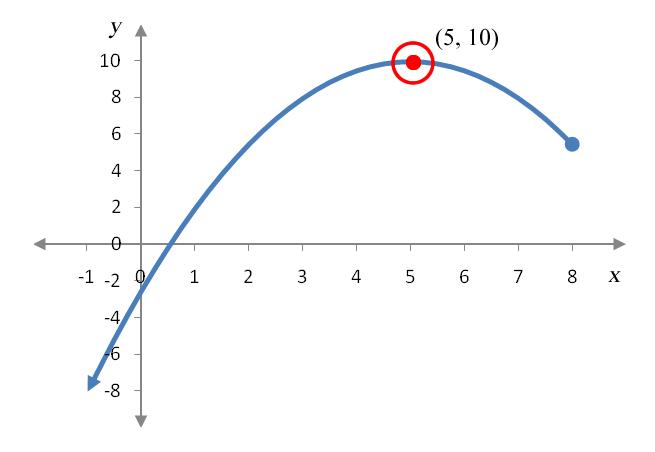
Solution Since the point (5, 10) is higher than any other points in an open interval centered on (5, 10), the relative maximum occurs at that point. There are no troughs in the function so there are no relative minima on the function over this interval.
A function’s absolute extremum occurs at the highest or lowest point on a function. The highest point on a function is called the absolute maximum and the lowest point on a function is called the absolute minimum.
Let f be a function defined on some interval and c be a number in that interval.
An absolute maximum of the function f occurs at (c, f (c)) if f (x) ≤ f (c) for every x value in the interval.
An absolute minimum of the function f occurs at (c, f (c)) if f (x) ≥ f (c) for every x value in the interval.
Example 3 Find the Absolute Extrema
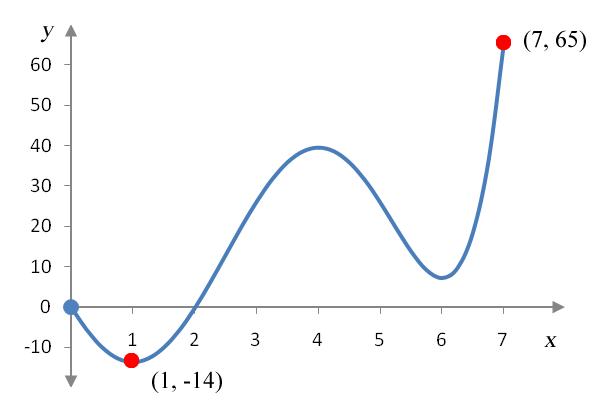
The function p(x) is defined on the interval [0, 7] in the graph below. Find all absolute extrema of p(x).
Solution The absolute extrema of p(x) are the highest and lowest points on the graph over the interval [0, 7].
The absolute maximum occurs at the point (7, 65) since it is higher than any other point on the function over the interval [0, 7]. The absolute minimum occurs at the point (1, -14) since it is lower than any other point on the function over the interval [0, 7].
Example 4 Find the Absolute Extrema
The function d(x) is defined on the interval (-∞, 8] in the graph below. Find all absolute extrema of d(x).
Solution Unlike Example 3, this function is not defined on a closed interval. From the graph, it is apparent that the highest point on the graph is (5, 10) so the absolute maximum occurs at that point. The graph continues downward on the left side (as evidenced by the arrow on the left side of the graph) so there is no lowest point. Therefore, there is no absolute minimum.
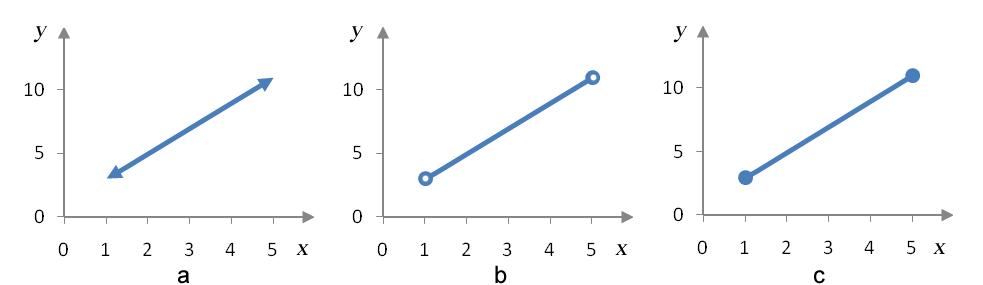
In general, a function may or may not have relative extrema or absolute extrema. Compare the three graphs in Figure 1. Since there are no crests or troughs on these linear functions, we cannot find an open interval around any points in the intervals that are higher or lower than points nearby. This indicates that there are no relative extrema on any of the graphs.
Figure 1 – A linear function defined on three different intervals. In (a), the function is defined for all real numbers. In (b), the function is defined on the open interval (1, 5). The function in (c) is defined on a closed interval [1,5].
In Figure 1a, there are no absolute extrema since the graph continues indefinitely up on the right side and indefinitely down on the left side. You might think that the lack of absolute extrema would be remedied by cutting the graph off at some values as in Figure 1b. The extreme values should be at the endpoints of the interval, but since the interval is an open interval, the endpoints are not included on the function.
In Figure 1b, we might try to say that the absolute maximum and minimum are very close to the ends of the interval, at x = 4.9 and x = 1.1. If this were the case, these x values would correspond to ordered pairs that are higher or lower than any other ordered pairs over the open interval. By inspecting the graph closely, we can see that the ordered pair corresponding to x = 4.99 is higher than the ordered pair for x = 4.9 and the ordered pair corresponding to x = 1.01 is lower than the ordered pair for x = 1.1. Since we can always move a little bit closer to the ends of the open interval, we’ll never be able to find a point we can call the highest or lowest. This can only happen for this function if it is defined on a closed interval as in Figure 1c.
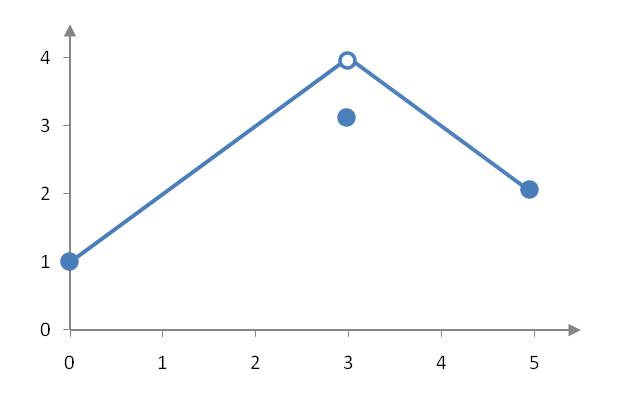
To guarantee an absolute maximum and absolute minimum on a function, it needs more than simply being defined on a closed interval. The function in Figure 2 has an absolute minimum at , but no absolute maximum.
Figure 2 – A discontinuous function defined on a closed interval [0,5].
There appears to be a highest point on the graph near (3, 4), but where? We could say it is at x = 2.9 or x = 3.1, but points closer to x = 3 like x = 2.99 are higher. In fact, the closer we get to x = 3, the higher the graph is. Since we would never be able to name a point that is highest, there is no absolute maximum.
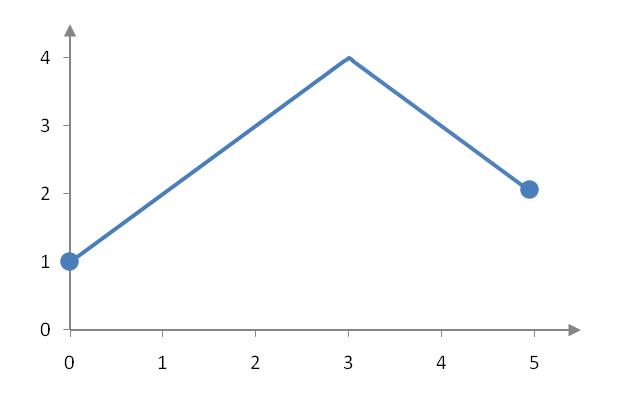
A closely related continuous function is graphed in Figure 3. The absolute maximum of this function occurs at (3, 4) since it is the highest point on the function over the closed interval [0, 5]. The absolute minimum of the function occurs at (0,1) since this point is the lowest point over the closed interval [0, 5].
Figure 3 – A continuous function defined on the interval [0,5].
The Extreme Value Theorem gives the conditions under which the absolute extrema are guaranteed.
Extreme Value Theorem
A function f that is continuous on a closed interval is guaranteed to have both an absolute maximum and an absolute minimum.
In the rest of this section, we’ll learn how to find absolute extrema and relative extrema of a function using the derivative of the function.