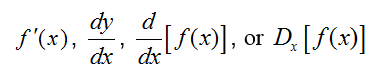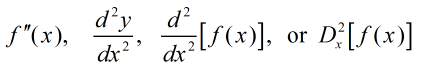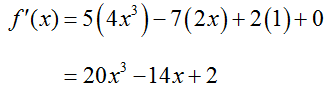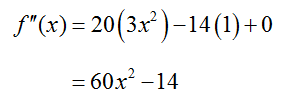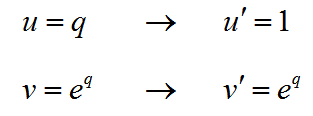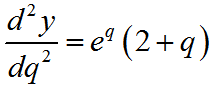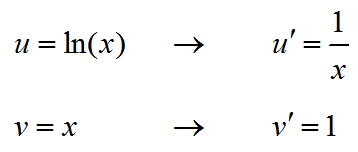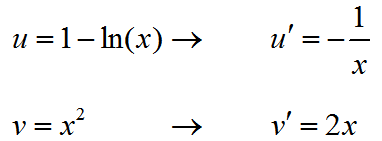How is the second derivative calculated?
The second derivative is the derivative of the derivative. To help identify this process, the first time we take a derivative of a function we call it the first derivative. The first derivative, as we have seen earlier, is symbolized in several different ways. If we take the first derivative of a function y = f (x), the first derivative is written as
Several notations for the second derivative are used.
Any of the following notations may be used to write the second derivative of a function :
We can take the derivative of the first derivative by applying the rules for derivatives to the first derivative. If f (x) = 5x4 – 7x2 +2x – 1, then we can apply the Sum / Difference, Product with a Constant, and Power Rules for Derivatives to yield the first derivative
If we use these rules again on the first derivative, we get the second derivative,
The process for finding the derivative is the same as we have used in Chapter 11. The only difference is the starting point. When finding the first derivative of a function, we take the derivative of the function. For the second derivative, we take the derivative of the first derivative.
Example 1 Calculate the Second Derivative
Let f (x) = x3 -4x2 + 6x +12. Find the second derivative f ″(x).
Solution The first derivative of is found by applying rules for derivatives,
To find f ″(x), take the derivative of f ′(x) = 3x2 – 8x +6:
The second derivative is f ″(x) = 6x – 8.
Example 2 Calculate the Second Derivative
Let
Find the second derivative 
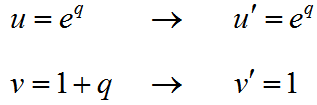
Solution The first derivative is found with the Product Rule for Derivatives using the factors
The first derivative is
Apply the product rule again to find the second derivative with the factors
The second derivative is
The second derivative is 
Example 3 Calculate the Second Derivative
Let 
Find the second derivative g″(x).
Solution Use the Quotient Rule for Derivatives to find the first derivative with
The first derivative is
To compute the second derivative, take the derivative of the first derivative with the Quotient Rule for Derivatives,
The second derivative is
The second derivative expression can be simplified further by factoring the numerator:
The second derivative is 