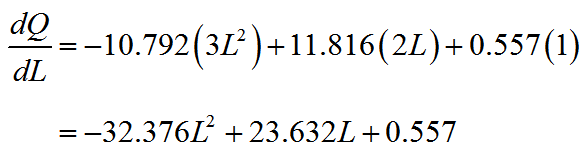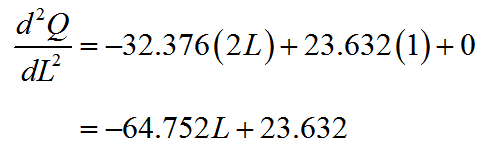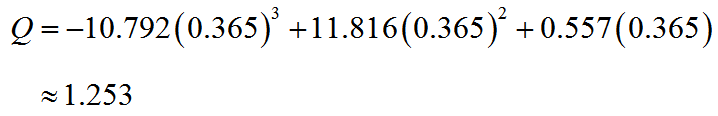What is the point of diminishing returns?
Many factors influence the output from a business. The quality and quantity of a particular type of technology might inhibit or enhance the output of a business. A company making leather wallets by hand will produce many fewer wallets in a given amount of time compared to a company that uses stitching and cutting machines to make the wallets. Similarly, utilizing more laborers allows a company to divide the tasks required for production among the employees so that each employee is able to specialize in a particular aspect of the production process. Such specialization allows the laborers to work more efficiently resulting in higher rates of production. However, too many employees results in overcrowding and eventually causes the output to increase at a lower rate. This pattern of production is the result of the Law of Diminishing Returns.
Law of Diminishing Returns
When an input is increased, such as labor, while all others are held constant, the resulting increase in production will become larger and larger until the point of diminishing returns. After the point of diminishing returns, the increase in production becomes smaller and smaller.
Since the Law of Diminishing Returns refers to changes in production as an input to production is changed, you would expect that we would be able to relate the derivative of the production function, marginal production, to the point of diminishing returns.
The top graph in Figure 7 shows a typical production function in which all inputs except one, like labor, are held constant. As the input is increased, the output increases at a greater and greater rate until the point of diminishing returns. After the point of diminishing returns, the output continues to increase but at a smaller and smaller rate.
The bottom graph in Figure 7 shows the derivative of the production function, marginal production. Since the point of diminishing returns occurs at the steepest point on the production function, the corresponding input on the derivative of the production occurs at a relative maximum.
To find this relative maximum, we need to find a critical value on the second derivative.
Figure 7 – (a) The production function
and (b) its first derivative.
The bottom graph in Figure 8 shows the second derivative of the production function. The critical value of the first derivative occurs where the second derivative is zero. The second derivative is positive on the left side of the point of diminishing returns and negative on the right side. This indicates that the derivative of the production function changes from increasing to decreasing. It also shows that the production function changes from concave up to concave down and has a point of inflection. So the point of diminishing returns on the production function is a point of inflection. We can use this fact to find the point of diminishing returns.
Figure 8 – (a) The production function
and (b) its second derivative.
Example 9 Find the Point of Diminishing Returns
If we assume labor is the only input to production that can be varied, the relationship between the number of barrels of beer Q (in millions) produced at the Boston Beer Company and the number of employees L (in thousands) from 2000 to 2007 is
Find the point of diminishing returns.
Solution The point of diminishing returns is obtained from the second derivative, 
by finding the point of inflection. The first derivative is easily calculated:
The second derivative is calculated by taking the derivative of the first derivative,
The point of diminishing returns occurs where the production function changes from concave up to concave down. For a continuous function like this one, this occurs when the second derivative changes from positive to negative. Set the second derivative equal to zero and solve for L to find where the concavity might change:
For this value to correspond to a point of diminishing returns, the function must change from concave up to concave down at this value. Test a value on either side of L ≈ 0.365 in the second derivative to yield the number line:
On the left side of L ≈ 0.365, the second derivative is positive so the function is concave up. The concavity changes on the right side of L ≈ 0.365 since the second derivative is negative in that interval.
This value is a point of diminishing returns and the number of barrels when the number of employees is 365 is
or 1,253,000 barrels of beer.