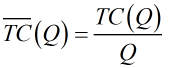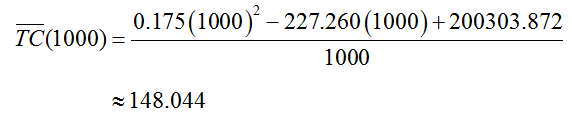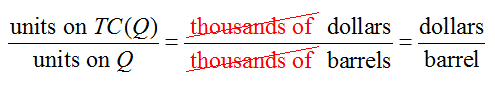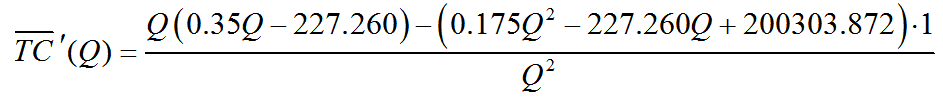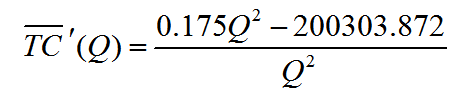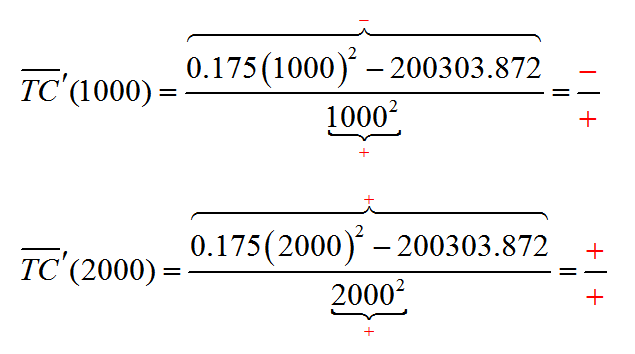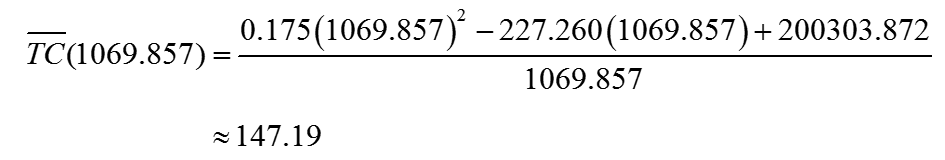How do you minimize the average cost for a business?
When businesses produce goods or services, they incur costs. As discussed earlier, these costs may be variable costs or fixed costs depending on whether the cost changes as the production changes. Whether a cost is variable or fixed depends on the time period over which the costs are analyzed. In the short run, at least one of the business’s inputs are fixed. For instance, its technology and size of the factory may be fixed and the number of workers may be variable in the short run. The fixed costs then correspond to the cost of the fixed inputs and the variable costs correspond to the cost of the variable inputs. In this text we look at costs primarily in the short run.
The time period over which all inputs may be varied is called the long run. In the long run, the business can vary any of its inputs. In this case, it may change its technology and change the size of the factory. The actual length of time that constitutes the long run varies from company to company. A restaurant may be able to increase the size of its kitchen or dining area in a few months while a semiconductor may need a year or more to change its manufacturing process.
The idea of optimizing costs is not a matter of minimizing costs. Since costs increase as production increases in the short run, the minimum total cost occurs at a production level of zero. Instead of minimizing the total cost, businesses minimize the average total cost.
The average total cost TC(Q) is defined by dividing the total cost function TC(Q) by the number of units produced Q,
Example 3 Minimize Average Cost
Based on data from 2000 to 2007 the total annual costs at the Boston Beer Company can be modeled by
where Q is the number of barrels of beer produced each year in thousands.
(Source: Modeled from Boston Beer Company Annual Reports)
a. Find the average total cost function .
Solution The average total cost function is calculated by dividing the total cost at some quantity by the quantity, . Using the cost function for the Boston Beer Company, we get
b. Find and interpret .
Solution The value TC(1000) is the average total cost to produce 1000 thousand barrels of beer. This value is calculated by substituting 1000 into TC(Q),
The units on this value are determined by dividing the units on the cost function by the units on the quantity. In this case, we get
The average cost when 1000 thousand barrels of beer are sold is 148.044 dollars per barrel. This means, on average, each barrel costs this amount to produce.
c. Find the production level that minimizes average cost.
Solution The relative minimum is found by locating all critical points and utilizing the first derivative test to classify the critical points. The derivative of 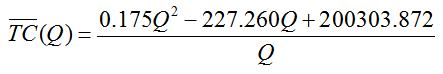
The derivatives
are easy to compute. The quotient rule yields
The numerator is simplified to give
This derivative will be used to find the critical values and to apply the first derivative test. The critical values are found by determining where the derivative is undefined or equal to zero. Since the denominator of the derivative, Q2, is equal to zero at Q = 0, there is a critical value there. However, a quantity sold of 0 thousand barrels is not a reasonable solution. In fact, the average cost function is undefined there so we ignore that critical point and restrict our attention to quantities sold Q that are positive.
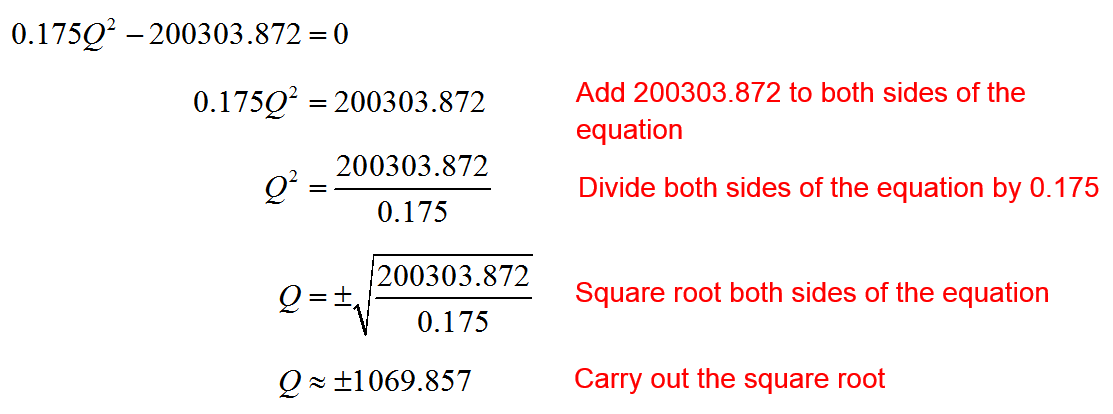
The derivative is equal to zero when the numerator is equal to zero. Set the numerator equal to zero and solve for Q:
To find the critical values, we must solve this equation for Q. We could utilize the quadratic formula, but it is easier to solve for Q directly.
Only the positive critical value is a reasonable production level for the Boston Beer Company.
This critical value may be a relative maximum or a relative minimum. The first derivative test allows us to classify the critical value by testing the first derivative on either side of the critical value.
For this function, quantities sold that are positive are the only allowable values. We begin the first derivative number line by restricting it to positive quantities.
Now let’s test the values Q = 1000 and Q = 2000 in the factors of the derivative. These values are picked because they are easier to determine the sign with:
Let’s record this information on the first derivative number line.
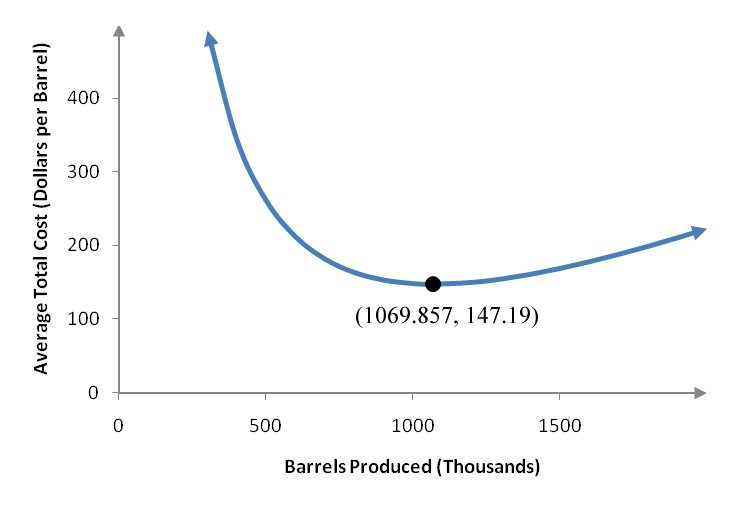
The graph of the average cost function is decreasing on the left side of the critical value and increasing on the right side. This tells us that the critical value is a relative minimum. To find the average cost at a production level of Q ≈ 1069.857, substitute the value into the average total cost function. This results in the lowest average total cost,
The average cost is minimized at a production level of 1,069,857 barrels and at an average total cost of 147.19 dollars per barrel