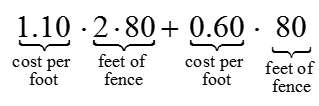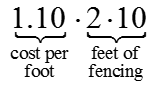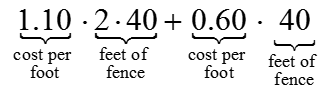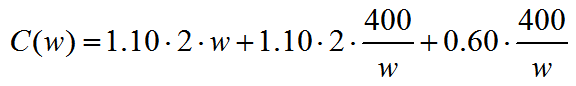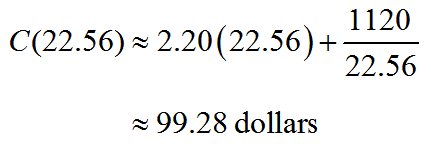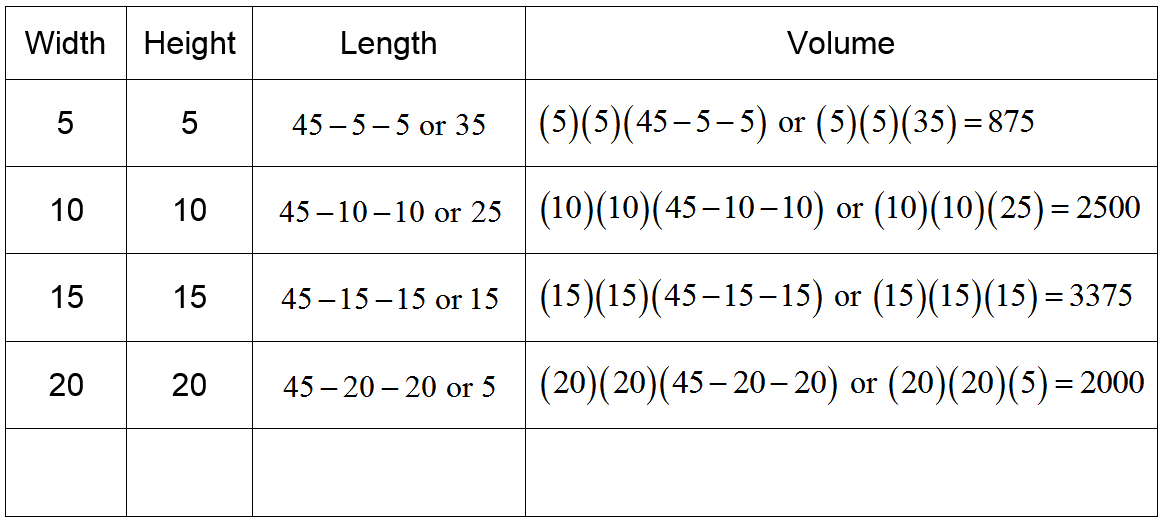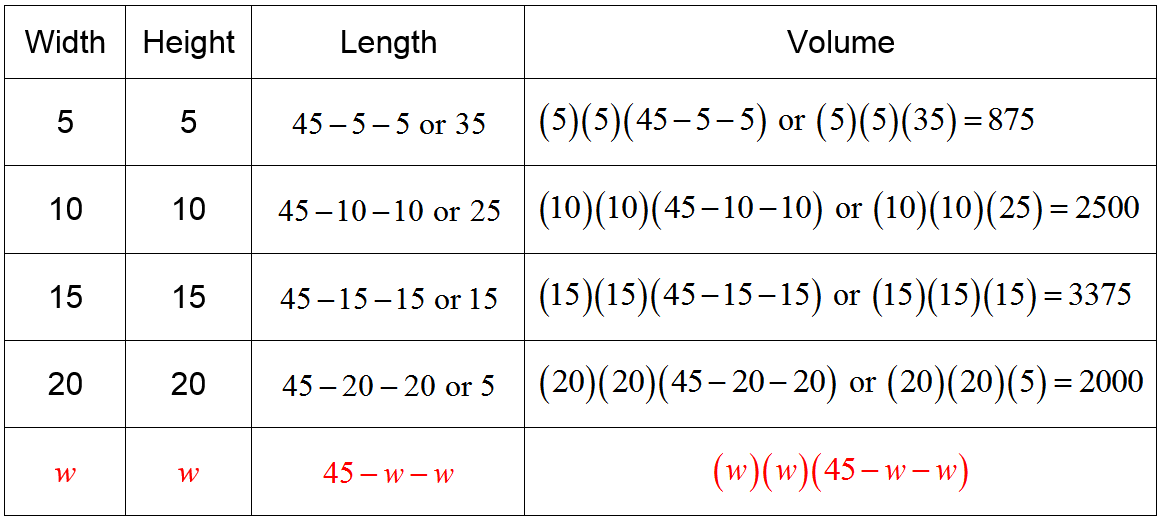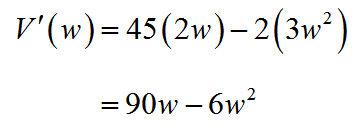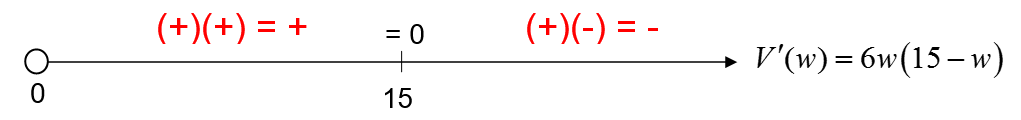How do you find the optimal dimensions of a product?
The size and shape of a product influences its functionality as well as the cost to construct the product. If the dimensions of a product are designed to minimize the cost of materials used to construct the product, then the objective function models the cost of the material in terms of the dimensions of the product.
In Example 1, we find an objective function for the cost of materials to build a rectangular enclose. By finding the relative minimum of this objective function, we are able to find the dimensions of the enclosure that costs the least amount.
Example 1 Minimize Cost of Materials
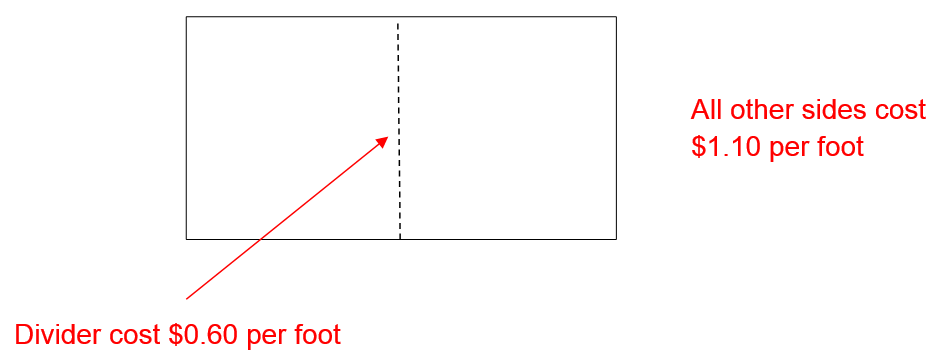
A farmer is fencing a rectangular area for two equally sized pens. These pens share a divider that will be constructed from chicken wire costing $0.60 per foot. The rest of the pen will be built from fencing costing $1.10 per foot.
If the pens should enclose a total of 400 square feet, what overall dimensions should the pens have to minimize fencing costs?
Solution To find the minimum fencing costs, we must formulate a function that describes the cost of fencing as a function of some variable. In this problem, we have two variables we could use. The width or length of the enclosed region can be the variable. In this example, we’ll choose the variable to be the width of the region.
Informally, the cost of fencing is
Cost = Cost of Width Components + Cost of Length Components
Each of these terms describes the cost of individual components of the fencing around the enclosed area. The first term matches the parts of the fencing along the top and bottom of the figure costing $1.10 per foot. The second term matches the two parts of fencing along the sides costing $1.10 per foot as well as the divider costing $0.60 per foot. A table is useful to help us recognize the function describing the cost of the fencing. In this table, each column will represent the quantities that will vary, the two terms in the cost of fencing as well as the total cost of fencing.
The table below contains five columns for these quantities and five blank rows in which we’ll place some values.
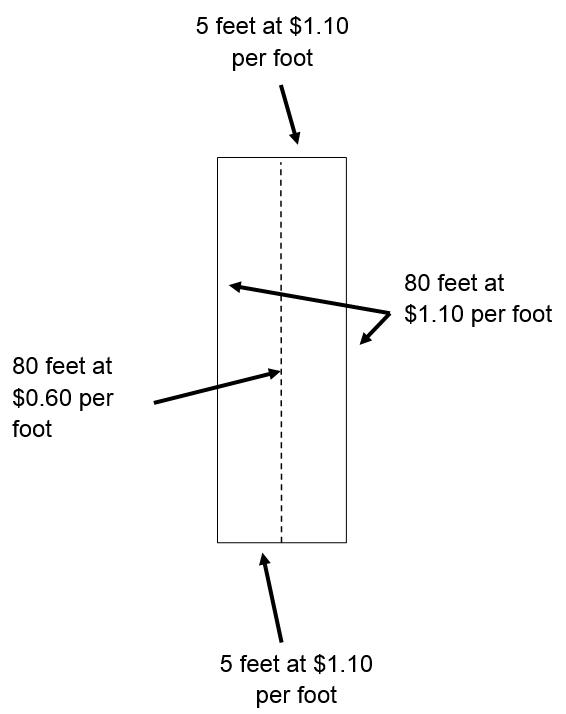
Start by entering several combinations for length and width that yield 400 square feet. For example, a pen that is 5 feet by 80 feet encloses 400 square feet. Another possibility is a pen that is 10 feet by 40 feet. In general, if the width is w then the length is 
.
Now let’s calculate the costs involved in fencing a pen that is 5 feet by 80 feet.
The width components will cost
and the length components will cost
to give a total cost of
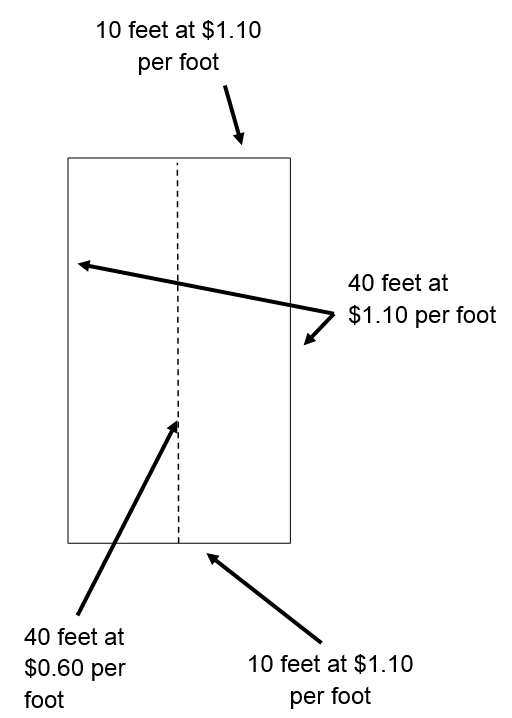
The cost involved in fencing a pen that is 10 feet by 40 feet is calculated in a similar manner.
The width components will cost
and the length components will cost
to give a cost of
This expression is almost identical to the earlier expression except amounts of fencing are different. We can continue to calculate other sized pens to fill out a table of values.
The last row in the table, the width is labeled as w and the corresponding length must be to ensure the area is 400. The other entries in the last row use the width and length to match the pattern in the rows above.
Based on this pattern, we can define the cost function C(w) as a function of the width w,
We can simplify the function to
We’ll need to take the derivative of this function to find the relative minimum. It is easiest to take the derivative with the power rule for derivatives if we rewrite the second term with a negative exponent. With this modification, the cost function is
The derivative is
To find the critical points, we need to find where the derivative is equal to zero or undefined. Set the derivative equal to zero and solve for w:
To solve this quadratic equation, we could use the quadratic formula. However, it is easier to isolate w2:
The negative critical value is not a reasonable dimension for the width of the pen so we can ignore it.
If the derivative is rewritten as 
, we observe that it is undefined at w = 0. Like negative values, a width of zero is not a reasonable dimension for a pen. Ignoring this value, we have only one critical value, w ≈ 22.56, in the domain of this problem.
This critical value may correspond to a relative minimum or a relative maximum. We can use the first derivative test to determine which type of extrema this critical value matches.
If we test the first derivative on either side of the critical value, we can establish where C(w) is increasing and decreasing.
This first derivative test indicates that the function is decreasing and then increasing so w ≈ 22.56 corresponds to a relative minimum.
The expression for the length is . Using the width, w ≈ 22.56 feet, the length is calculated as approximately 17.73 feet. These dimensions yield a minimum total cost of
For some businesses, the goal of the design process is not a product that costs as little as possible. Instead, they maximize or minimize some characteristic of the product with respect to the dimensions of the product. For instance, a newspaper publisher might maximize the area of the printed page with respect to the margins and dimensions of the page. By doing this, they maximize the area used to print news as well as the area used for advertisements.
In the next example, we find the dimensions a piece of carry-on baggage that maximizes the volume inside the bag and meets airline requirements for the dimensions.
Example 2 Maximize Volume
Most airlines charge to check baggage on flights. To avoid these charges, passengers pack as much as possible into their carry-on bags. However, airlines also limit the size of these bags. American Airlines limits the linear dimensions (defined as the sum of the length, width and height) to 45 inches.
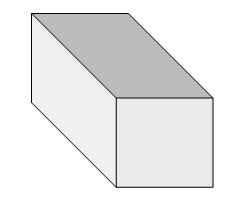
A manufacturer wishes to produce a carry-on bag whose linear dimensions are 45 inches. The shape of the bag is a rectangular solid, like the one pictured, below whose ends are squares.
What are the dimensions of the bag if its volume is to be as large as possible?
Solution We want to maximize the volume of the carry-on bag. To help us understand the relationships between the dimensions, let’s look at a particular carry-on bag. Suppose the dimensions of the square ends are 5 inches by 5 inches. Since the sum of the length, width, and height must be 45 inches, we know the length must be 45 – 5 – 5 = 35 inches.
The volume of this carry-on bag is the product of the length, width, and height so this bag is
Let’s look at a second possibility. Suppose the dimensions of the square end are 10 inches by 10 inches. The length must be inches. The volume of this carry-on bag is
Notice that these dimensions result in a larger volume.
We can continue this process to see if the volume continues to increase as the square end gets larger. To keep track of the information, let’s enter this information into a table.
As the dimensions of the square end increases, the volume rises and then falls. It appears that the optimal dimensions are around 15 inches by 15 inches by 15 inches.
To find a more exact answer, we need to come up with an expression for the volume. We do this by identifying the variable as the width w and look for pattern in each column of the table.
If the width corresponds to w, so must the height since the ends are square. If we subtract these dimensions from 45, we get the length . The volume is the product of these dimensions.
Using this pattern, define the volume V as
This simplifies to
It is much easier to take the derivative of this function once it has been simplified. Using the basic rules for derivatives, the derivative is calculated as
This derivative is set equal to zero to find the critical values for the function. Since the derivative is a polynomial, there are no values of w for which the derivative is undefined. Additionally, all critical values must be positive since the width must be a positive number.
Set the derivative equal to zero and solve for w:
Only the critical value at w = 15 is a reasonable dimension of the carry-on. Now let’s use the first derivative test to determine if the critical value is a relative minimum or a relative maximum:
The volume function increases initially and then decreases after w = 15. This matches the behavior we saw in the last column of the table. It also tells us that the critical value corresponds to a relative maximum. The optimal solution occurs when the square end is 15 inches by 15 inches and the length is 45 – 15 – 15 or 15 inches. The volume at these dimensions is (15 inches)(15 inches)(15 inches) or 3375 in3.