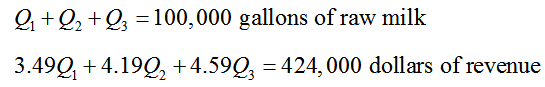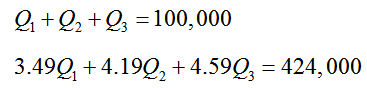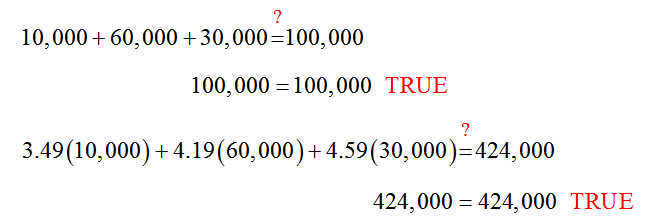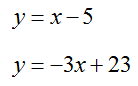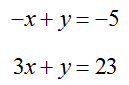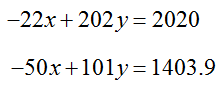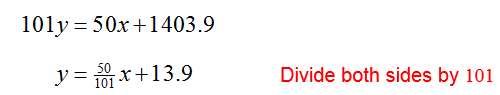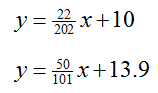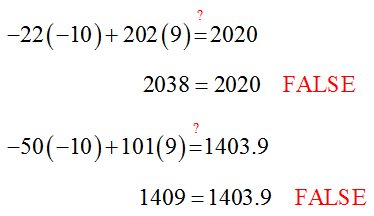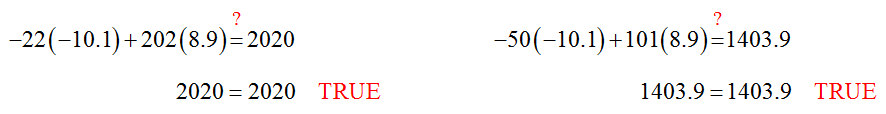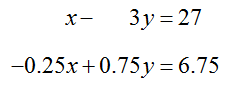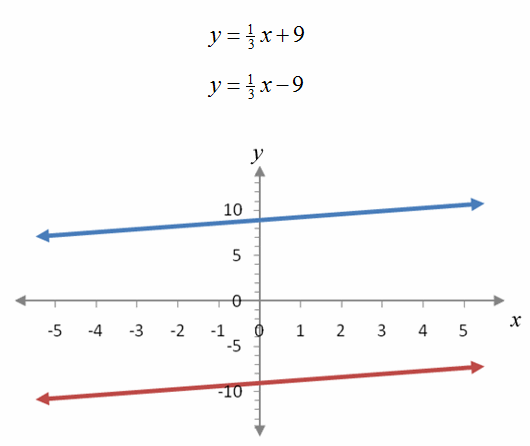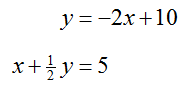What is a system of linear equations?
In many applications there is more than one equation that governs the solution to the problem. For instance, suppose we want to process 100,000 gallons of raw milk into whole, 2%, and 1% milk. Each type of milk sells for $3.49, $4.19 and $4.59 per gallon respectively. The dairy needs $424,000 in revenue from the sale of the milk. If Q1, Q2, and Q3 are the amounts of whole, 1% and 2% milk processed in gallons, the solution to this problem must satisfy
By using the term “satisfy”, we mean that when values are substituted into the variables Q1, Q2, and Q3, the left hand side of each of the equations is equal to the right hand side of the same equation. When the two sides of the equation yield the same values, we say that the values result in a true statement. If the values substituted into the equation result in different values on each side of the equation, we say that the values result in a false statement. There are two equations for this problem since the dairy wants to use all of the raw milk and have $424,000 in revenue from the sales of the processed milk. Any combination that allows the dairy to meet both of these requirements is a reasonable solution to this application.
To check whether there exists a combination of milk products that works, we need to substitute values for the variables into each equation.
Example 1 Do Specific Combinations Solve Both Equations?
For each part below, determine if the combination of milk is a solution to the equations
where Q1, Q2, and Q3, are the amounts of whole, 1% and 2% milk processed in gallons.
a. 50,000 gallons of whole milk, 50,000 gallons of 1% milk and no 2% milk.
Solution For this combination of milk, we have Q1 equal to 50,000, Q2 equal to 50,000, and Q3 equal to 0. If we substitute these values into the first equation, we get
50,000 + 50,000 + 0 = 100,000 TRUE
Since the left hand side of the equation is equal to 100,000, this combination of milk results in a true statement and combines to give the proper amount of milk. However, when we put this combination of milk products in the second equation, we get
3.49(50000) + 4.19(50,000) + 4.59(0) 424,000 FALSE
The left hand side of the equation simplifies to 384,000 to yield a false statement. This combination of milk products does not solve the second equation. This combination solves the first equation so the amounts total to 100,000 gallons of milk, but does not solve the second equation. The amount of revenue from the sales does not equal $424,000.
b. 10,000 gallons of whole milk, 60,000 gallons of 1% milk and 30,000 gallons of 2% milk.
Solution Put the values Q1 = 10,000, Q2 = 60,000, and Q3 = 30,000 into each equation:
yields two true statements. Since this combination makes each equation true, we know that it gives both the proper amount of milk and the proper revenue.
For this set of equations, each variable was raised to the first power so the equations are linear in each variable. When the combination of values solves each of the linear equations, the values for the variables are a solution to the system of linear equations formed by the two equations.
Let’s generalize these ideas to help us understand exactly what a system of linear equations is. A system of linear equations consists of several equations containing variables and constants. Recall that variables are letters or symbols that represent unknown quantities. In any of the linear equations, the variables can vary. Constants are values that do not change in an equation. Constants may be numbers like 3 or –5. Or a constant may be a letter that represents a fixed but unknown number.
As illustrated in Example 1, the equations in a system of linear equations can have any number of variables. It is best to name them in a systematic way. Since we were referring to quantities of milk, the letter Q was useful. There were three variables so subscripts distinguish each type of milk and yield Q1, Q2, and Q3.
For business problems we need to allow for any number of variables representing a variety of quantities. We could use variables without subscripts like x and y, but we would run out of names quickly for most realistic applications. If we use the letter x, n variables are represented by x1, x2, …, xn. Letters representing constants can be handled in a similar manner. We can represent n constants using the letter a as a1, a2, …, an. The single constant on the right side of a linear equation is represented by the letter k. With these constants and variables, a definition for a linear equation can be written. Keep in mind that there is nothing special about the letters used and any letter could be used in place of a, k or x. However, since a1, a2, …, an and k are constants, these letters represent fixed values. This makes them different from the variables x1, x2, …, xn which represent values that can vary in the equation.
A linear equation in n variables x1, x2, …, xn is any equation that can be written in the form
Two special cases must be noted. Many simple problems involve only two variables. We could write the linear equation as a1x1 + a2x2 = k, but often the letters a, b, x, and y are used. An equivalent linear equation in two variables is ax + by = k . Similarly, for three variables you can write a1x1 + a2x2 + a3x3 = k or ax + by + cz = k. For more than three variables we run out of letters at the end of the alphabet and resort to subscripts. The key concept is that each term in the equation has first degree. Another way to say this is that the variable in each term is raised to the first power. As long as each term is a first degree term, the equation is called a linear equation.
If we collect several linear equations in the same variables together, we get a system of linear equations.
A system of linear equations in n variables is a finite number of equations where each equation can be written in the form
A solution to the system is a collection of values for the variables that makes all of the equations true.
Example 2 Do Certain Values Solve the System of Linear Equations?
The equations
form a system of linear equations since the collection of equations can be written as
Do the values x = 7 and y = 2 solve the system?
Solution To see if the values solve the system, we need to put the values into each equation and make sure both equations are true.
Since both equations are true, the values x = 7 and y = 2 solve the system of linear equations.
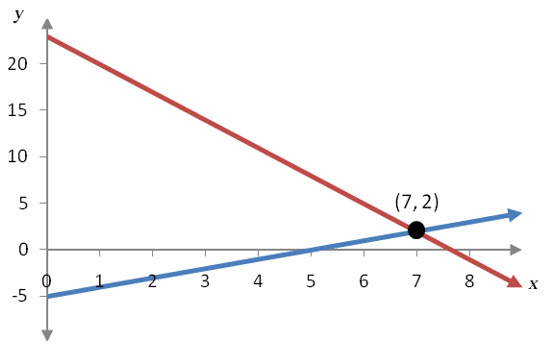
It is convenient to think of this solution in Example 2 as an ordered pair (x, y) and to write the solution as (7, 2). There is a good reason for doing this. The equations in Example 2,
both have graphs that are lines. These lines intersect at the solution to the system of linear equations. The first equation corresponds to a line with a slope of 1 and a vertical intercept of -5. The second line has a slope of -3 and a vertical intercept of 23.
Figure 1 – The two lines corresponding to the system of linear equations intersect at the solution (7, 2).
Graphing each equation is a simple way of estimating the solution to a system of equations. If the system of equations contains only two variables, the solution to the system is the point of intersection of all lines in the system if such a point exists.
Example 3 Find the Point of Intersection
Find the solution to the system of equations
by finding where the graphs of the equations intersect.
Solution To graph each equation, solve it for y. For the first equation,
To solve the second equation in the system for y,
The system can now be written as
Each of these equations is in the slope-intercept form for a line, y = mx + b. In this form, m is the slope of the line and b is the vertical intercept of the line.
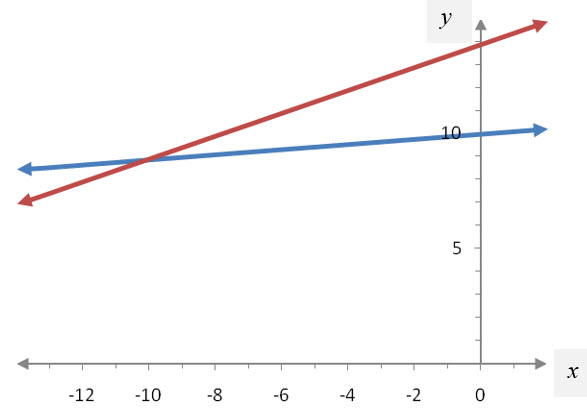
Figure 2 – A graph of the system in Example 3.
It is a good idea to make sure the lines are graphed properly. The blue line has a vertical intercept of 10 and a slope that is small and positive, 22/202 ≈ 0.11. The red line has a vertical intercept of 13.9 and a slope that is larger, 50/101 ≈ 0.50. Because the slope of the red line is larger than the slope of the blue line, the red line is steeper than the blue line.
Based on the graph in Figure 2, the point of intersection appears to be about (-10, 9). However this can’t be correct since and do not satisfy the two equations in the system.
The best we can say, based on the graph, is that the solution is close to (-10, 9). We’ll need to use a graphing calculator or algebraic techniques to be more precise. However, keep in mind that a graphing calculator will give a better answer, but is still an approximation. Algebraic techniques give the exact answer as long as numbers are not rounded in the process of finding the point of intersection.
By substituting these values into the system of equations, we can determine that these values are the exact solution:
When utilizing technology to find a solution, keep in mind that the solution is only an estimate unless the solution satisfies each equation in the system.
Each of the linear systems of equations we have considered has a single point of intersection. You can easily imagine a situation where two lines do not intersect. A system of equations for which the graphs do not intersect has no solutions.
Example 4 Find the Solution to the System of Equations
Solve the system of equations
by graphing both equations on the same graph.
Solution To graph each equation, we need to solve each equation for y.
When each equation is solved for y, we get an equivalent system of equations,
Figure 3 – A system of equations whose graphs are parallel.
Examining this system, we see that the slope of each line is 1/3 and the y intercepts are different. The lines in the system, graphed in Figure 3, are parallel and so the system has no solution.
Example 5 Find the Solution to the System of Equations
Graph the system of linear equations
to find the solution of the system.
Solution The first equation is already solved for y, but the second is not. Start by solving the second equation for y:
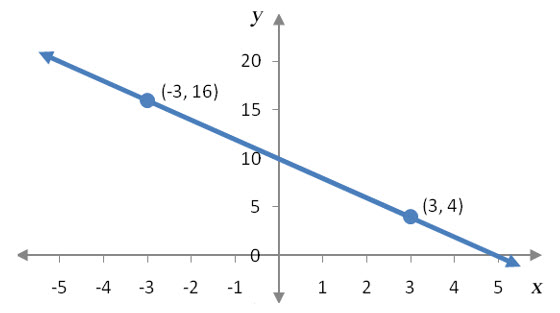
This equation is identical to the first equation so its graph is the same as the first equation. In other words, the two equations are different descriptions of the same line.
Figure 4 – The graphs of the two equations in Example 5 coincide everywhere along the line.
Any point on the line is a solution to the system of equations. For instance, the ordered pair (-3, 16) is a solution,
as well as the ordered pair (3,4):
We can symbolize this fact by writing the solution as any ordered pair (x, y) such that y = -2x + 10. Since both equations represent the same line, we could also say that the solution is any ordered pair (x, y) such that x + 1/2 y = 5.