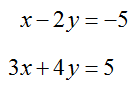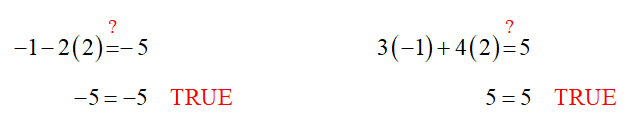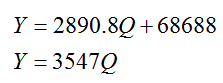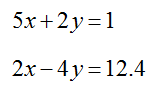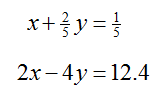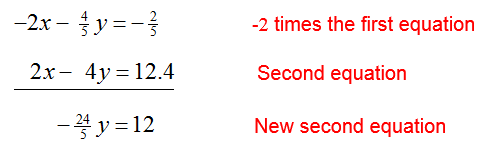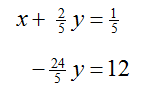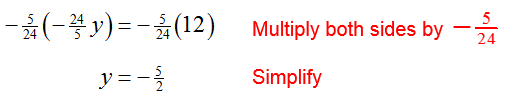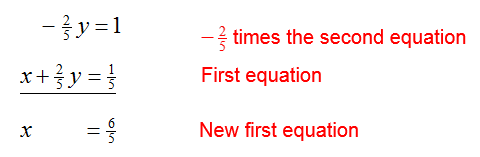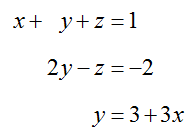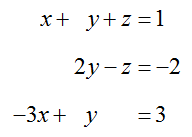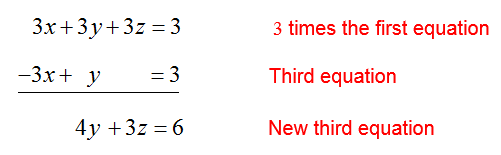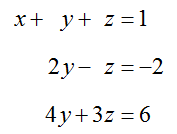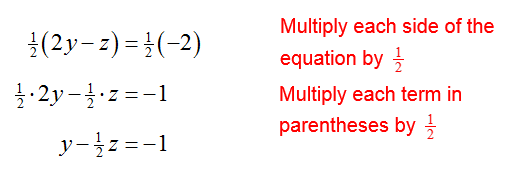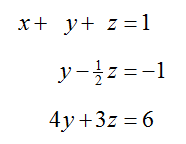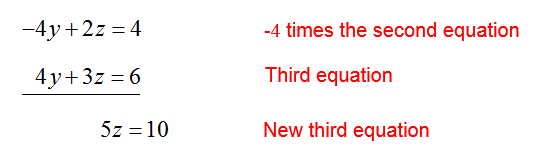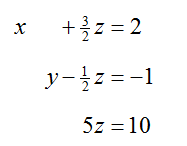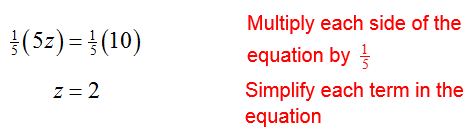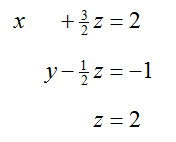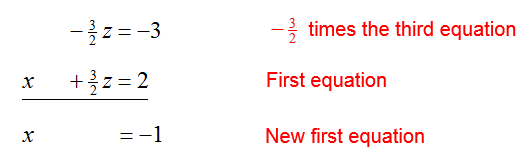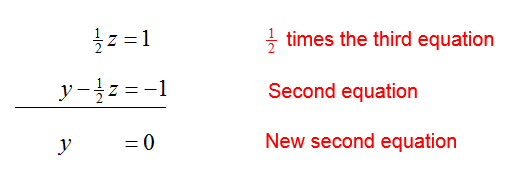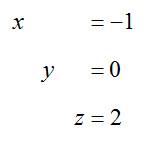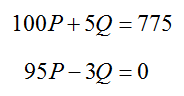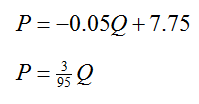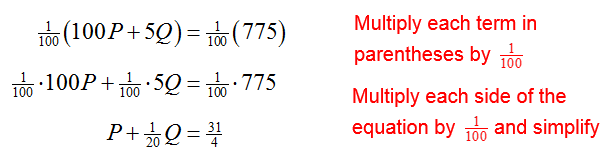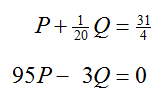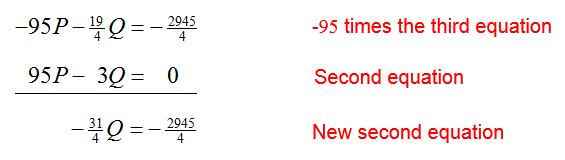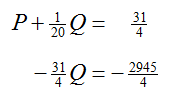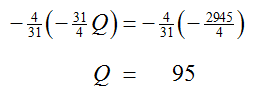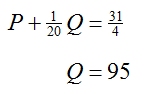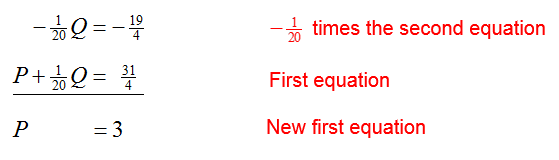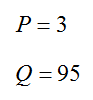How do you solve a system of linear equations?
There are two basic strategies for solving a system of two linear equations and two variables. In each strategy, one of the variables is eliminated allowing us to solve for the remaining variable. These two strategies are called the Substitution Method and the Elimination Method.
Although the Substitution Method may be used to solve a system in any number of variables with any number of equations, we’ll use the Substitution Method for systems of two equations in two unknowns. The Elimination Method may also be used to solve systems of equations in two variables. Additionally, the Elimination Method can easily be scaled up to solve systems of equations with more than two variables.
Substitution Method
- Solve for one of the variables in one of the equations. If it is difficult to solve for a variable, the Elimination Method may be better suited to solve the system.
- In the other equation, replace the variable you solved for in step 1 with the equivalent expression. Once you have replaced the variable in the other equation, there should only be one variable in this equation.
- Solve the equation containing only one variable for that variable.
- To find the value of the other variable, place the value obtained in step 3 into the equation from step 1.
Example 1 Find the Solution to the System
Solve the system of linear equations
using the Substitution Method.
Solution Using the first equation, solve for x. Add 2y to both sides to yield x = 2y – 5. Replace x with 2y – 5 in the second equation and solve for y:
The value for x is found by substituting y = 2 into the equation x = 2y – 5. This gives x = -1. The solution to the system is (x, y) = (-1, 2).
We can check the solution by substituting the solution into the original system:
Since the ordered pair makes both equations true, we have found the solution to the system.
In Example 6 of section 2.1, we found the point of intersection of the system of equations
Recall that the first equation describes the total cost Y for operating a dairy with Q cows. The second equation describes the total revenue Y for a dairy with Q cows. When the total revenue and total costs are equal, the business is at the break-even point. This point can be found graphically by locating the point of intersection on the total cost and total revenue graphs. The same point can be found algebraically using the Substitution Method. This strategy is ideal for this system since one (in this case, two) of the equations in the system is in slope-intercept form and solved for a variable.
Example 2 Dairy Break-Even Point
Solve the system of equations
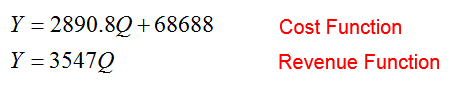
Solution Since each equation is solved for a variable, Y, we can replace that variable in the first equation with the equivalent expression from the second equation:
3547Q = 2890.8Q + 68688
To solve for Q:
The corresponding value for Y is Y ≈ 3547(104.68) ≈ 371,299.96. This tells us that break-even quantity is 104.68 cows and yields revenue and costs of about $371,299.96.
When it is not easy to solve for a variable, the Elimination Method can be used to eliminate a variable from the system of two equations. The Elimination Method relies upon the concept of equivalent systems of equations. Two systems of equations are equivalent if they share the same solution. A system of equations can be transformed to an equivalent system of equations using equation transformations.
A system of equations can be transformed to an equivalent system of equations by
- switching the positions of any two equations;
- multiplying each term in an equation by a nonzero number;
- replacing any equation in a system with the sum of one of the equations multiplied by a nonzero number and another equation multiplied by a nonzero number.
Using these three transformations, we can change a given system to a simpler system whose solution is easy to identify. These transformations can be applied to a system of equations in two variables or more than two variables.
Elimination Method
- Write each equation in the system with the variables on the left side and the constants on the right side of the equation.
- Rearrange the terms on the left side of the equation so that the variables appear in the same order in each equation. Write the terms so that each term with a specific variable is vertically align with terms containing the same variable.
- Multiply the first equation by the reciprocal of the coefficient of the first term (the leading coefficient). After this transformation, the coefficient of the first variable in the first equation should be a 1.
- Eliminate the first variable from all equations except the first equation using equation transformations.
- Multiply the second equation by the reciprocal of the leading coefficient. After this transformation the leading coefficient of second equation should be a 1.
- Eliminate the variable corresponding to the leading coefficient from all other equations except for the second equation.
- Continue this process for each equation and leading coefficient.
- Solve each equation for the leading variable to yield the solution to the system of equations.
Example 3 Find the Solution to the System
Solve the system of linear equations
using the Elimination Method.
Solution This system already has the variables on the left side of the equations and the constants on the right side of the equation. The terms are aligned so that each variable on the left side appears below terms with the same variable.
To make the coefficient of x in the first equation a 1, multiply the first equation by the reciprocal of 5 or 1/5
If we replace the first equation with this multiple of the first equation, we get the equivalent system of equations
Now that the leading coefficient in the first equation is a 1, eliminate x from the second equation. To do this, replace the second equation with -2 times the first equation added to the second equation:
Replace the second equation with this sum to yield the equivalent system of equations,
The leading coefficient of the second equation is – 24/5. To change the leading coefficient to a 1, multiply the second equation by – 5/24 :
Put this equation in place of the second equation to give the equivalent system of equations,
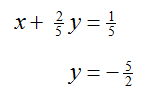
Replace the first equation with this sum to yield an equivalent system of equations,
Since this system is equivalent to the original system of equations, the solution to the original system of equations is (x, y) = (6/5, – 5/2) .
Example 4 Find the Solution to the System
Solve the system of linear equations
using the Elimination Method.
Solution This system of three equations has three variables and each equation does not have all three variables. However, this does not change the strategy introduced earlier. Before we can transform the equations to eliminate variables, we need to move all variable terms to the left side of the equations and constants to the right side of the equations. Subtract from both sides of the third equation and align the variables to give the system
Notice how each variable lines up vertically. If a variable is missing, we simply insert a space to insure all variables are properly positioned.
The leading coefficient in the first equation is a 1, so we need to eliminate x from all other equations.
To eliminate x from the third equation, multiply the first equation by 3 and add it to the third equation:
Replace the third equation in the system of equations with this sum,
Multiply the second equation by the reciprocal of its leading coefficient, 1/2:
Put this equation in place of the second equation to give an equivalent system of equations,
To eliminate y from the first and third equations,
Replacing these new equations in the system of equations give the equivalent system,
The leading coefficient of the third equation is changed to a 1 by multiplying the third equation by 1/5,
Replace the third equation with this new equation to give
To finish the transformations, we must eliminate z from the first and second equations:
Replacing these new equations in the system leaves us with
Since this system is equivalent to the original system, the solution is (x, y, z) = (-1, 0, 2).
The supply and demand curve for the dairy can be written as the system of equations
In this system of equations, the first equation corresponds to the demand function. This line relates the price P to the quantity of milk Q demanded by consumers at that price. The second equation, the supply function, relates the quantity of milk Q that suppliers are willing to supply at a price P. This system is equivalent to the system
that we found for dairies in Chapter 1.
Example 5 Find the Dairy Equilibrium Point
Find the equilibrium point by solving the system of equations
using the Elimination Method.
Solution To solve the system, we need to use equation transformations to change the leading coefficient of the first equation. By multiplying the first equation by 1/100, the leading coefficient becomes a 1:
Replace the first equation in the system with the new equation to yield an equivalent system of equations:
Now we must eliminate P from the second equation. The sum of -95 times the first equation added to the second equation is
Replace the second equation in the system with this new equation:
The leading coefficient of the second equation is changed to a 1 by multiplying both sides of the equation by – 4/31:
Replace the second equation with this new equation to give an equivalent system,
Finally, eliminate Q from the first equation.
Placing this equation in the system, we get
So the solution to this system is (Q, P) = (95,3) meaning that at a price of $3 per gallon the quantity demanded by consumers is 95 thousand gallons.