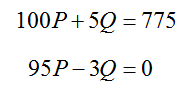Systems with Many Solutions or No Solutions
In all of the examples so far, each of the systems resulted in a unique solution. By this we mean a single value for each of the variables solved the system of equations.
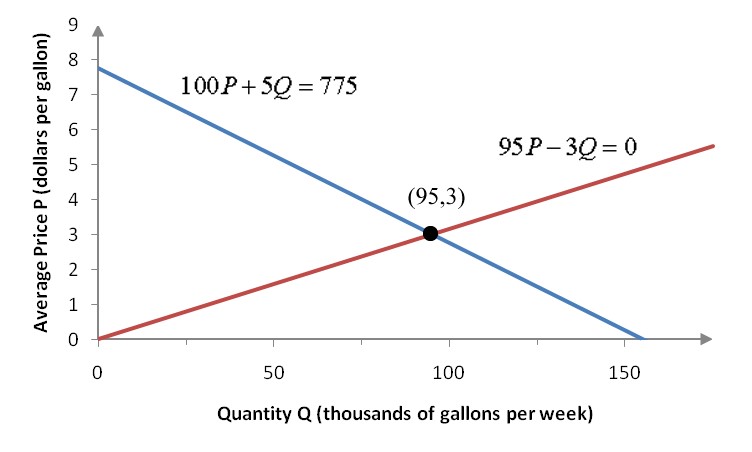
Figure 1 – A graph of the system in Section 2.1.
In Example 7 of Section 2.1, the solution (Q, P) = (95, 3) solved the system
Although the solution to the system is two numbers, there is only one ordered pair that corresponds to the solution. On a graph, this ordered pair matches the point of intersection of two lines.
In this section, we’ll examine systems which do not fit this pattern. In one type of system, there are no places on the graph where all of the lines intersect. These systems have no solutions.
For the other type of system, the lines in the system intersect at more than one ordered pair. This means that there are several solutions to the system. These systems have nonunique solutions. At the end of this section, we’ll examine how to mix different grade of ethanol to obtain a different grade of ethanol.
Read in Section 2.3
- Does every system have a unique solution?
- Handout: System of Two Equations in Three Unknowns
- How do you solve a system of three equations in two variables?
- How do you set up and solve an application involving systems of equations in two variables?
Section 2.3 Workbook (PDF) – 9/2/19