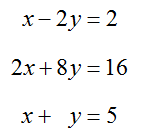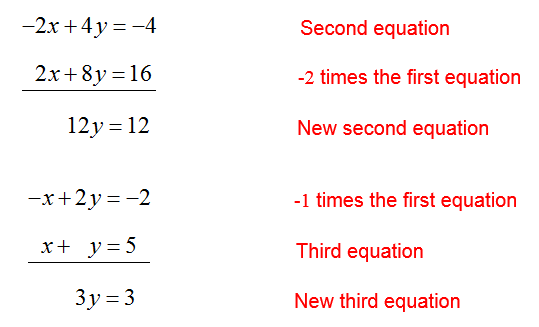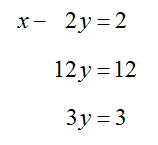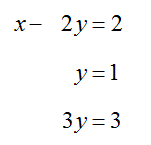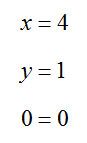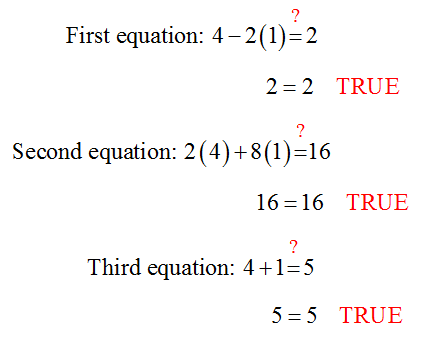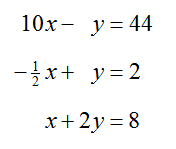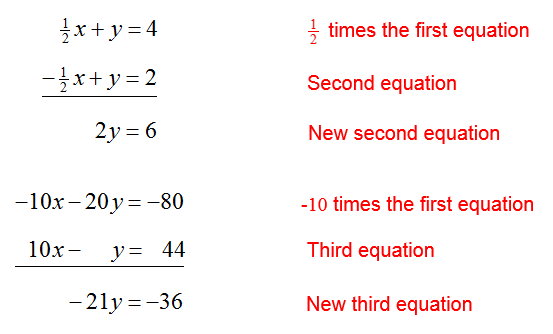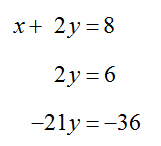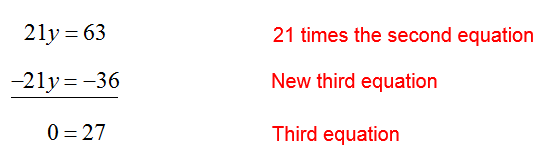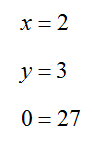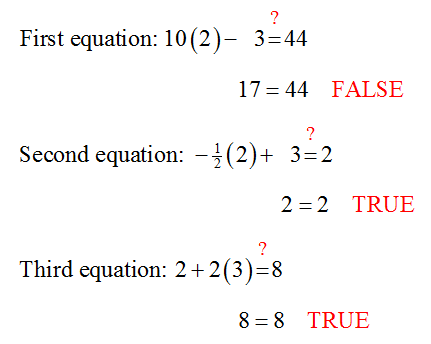How do you solve a system of three equations in two variables?
To solve a system of three equations in two variables, we extend the Substitution and Elimination Methods introduced earlier. A third equation in two variables simply adds a third line to the system. A solution to the system is an ordered pair that solves all of the equations in the system.
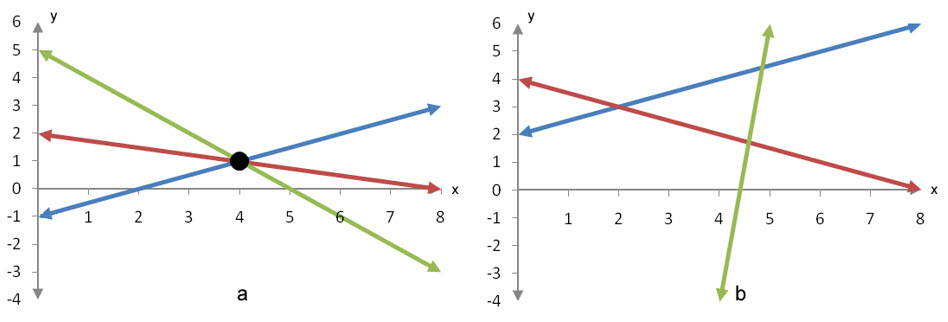
Figure 3 – Two systems of three equations in two variables. In Figure 4a, the solution to the system is (4,1). In Figure 4b, there is no solution since all three lines do not intersect at a single point.
Graphically, this is a point of intersection where all of the lines intersect. In Figure 3a, three lines are graphed corresponding to the three lines in a linear system. All of the lines intersect at the point (4, 1) which means it satisfies each of the equations in the system. If you consider only two of the lines in the system and use the Substitution Method or the Elimination Method, the resulting solution will also satisfy the third line in the system.
The system in Figure 3b has several points, such as (2, 3), where two of the lines in the system intersect. If you use the Substitution Method or the Elimination Method on these two lines, you would find a solution of x = 2 and y = 3. However, if this ordered pair is substituted in the other equation in the system, it will not be satisfied. This means that there is no ordered pair that satisfies all three equations simultaneously so the system is inconsistent.
Example 3 Find the Solution to the System
Solve the system
Solution Although we could use the Substitution Method to solve this system, the Elimination Method will be used in this example since it generalizes to larger systems much more easily. The leading coefficient of the first equation is already a 1, so we need to eliminate x from the other two equations.
Replace the second and third equations in the original system of equations with these new equations to give
Multiply the second equation by 1/12 to give the equivalent system of equations,
To complete the Elimination Method, we need to eliminate y from the first and third equations:
This helps us to write the equivalent system of equations,
The last equation is an identity which means it is always true. The first two equations indicate that the solution to two of the equations is (x, y) = (4,1). This and the identity indicate that this ordered pair also solves the third equation. We can check this by substituting into each equation:
Since (x, y) = (4,1) satisfies each equation in the system, it is the solution to the system of equations. Furthermore, since the first two equation specify a unique solution and not a relationship between the variables, this is the only solution to the original system of equations.
Example 4 Find the Solution to the System
Solve the system
Solution Start by solving any two of the equations for a solution. The Elimination Method provides a systematic approach for solving this system. To make the leading coefficient on the first equation a 1, interchange the first and third equation to yield
Now eliminate x from the second and third equations:
Replace the second and third equations with these new equations to give an equivalent system of equations,
Multiply the second equation by 1/2 to change the leading coefficient of the second equation to a 1. This leaves us with the equivalent system of equations,
Finally, eliminate x in the first and third equations:
Use these new equations to write the equivalent system of equations,
This indicates that (x,y) = (2,3) satisfies two of the equations, but not the third. The third equation is a contradiction. So the system is inconsistent and has no solutions. If we substitute into the original system of equations, we can discover which equations are satisfied and which are not:
The strategies in Example 3 and 4 can be applied to a system of any number of equations in two variables. If you use the Substitution Method, find the solution to two of the equations and then check it in each of the other equations. A solution to the system will satisfy all of the equations in the system. If the solution from any two equations does not work in all of the other equations in the system, the system does not have any solutions. If you use the Elimination Method, follow the strategy and look for the transformations to yield new equations that are contradictions (the original system has no solutions) or identities (the original system has many solutions). Remember, contradictions are equations like 0 = 27 that are never true and identities are equations like that are always true.