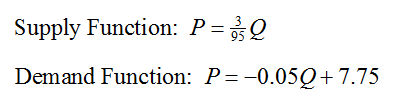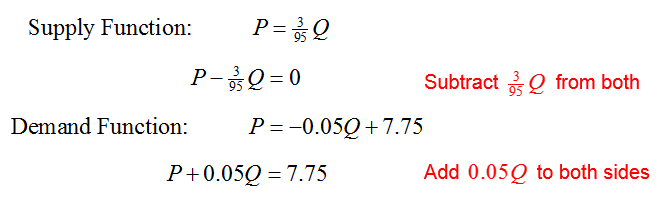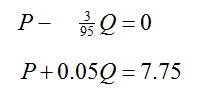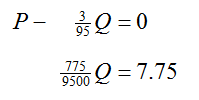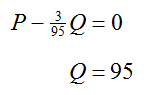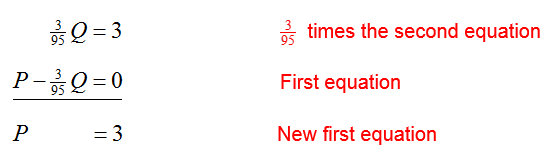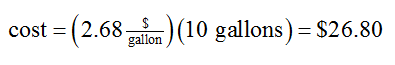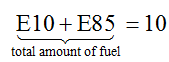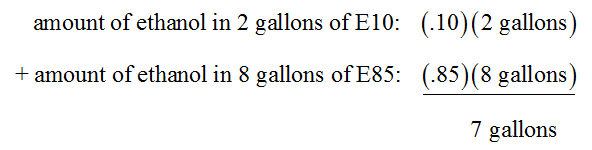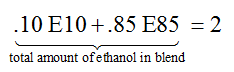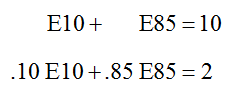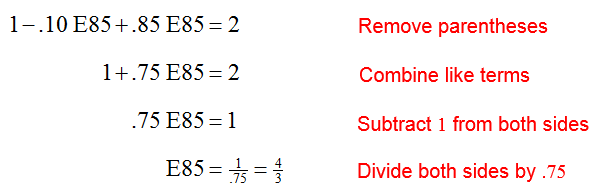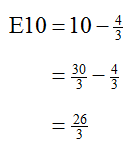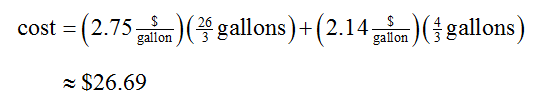Section 2.3 Question 3

How do you set up and solve an application involving a system of equations in two variables?

In section 2.1, we examined how the equilibrium point for the dairy industry could be found from the demand and supply functions from Chapter 1. In that section, we used a graph of the functions to locate the equilibrium point. The Substitution Method and Elimination Method can also be used to find the equilibrium point algebraically.

Example 5    Use the Substitution Method to Find the Equilibrium Point

The demand and supply functions for the dairy industry are described by

Use the Substitution Method to find the equilibrium point for this system of equations.

Solution Since one of the equations (in this case both) is solved for a variable, this system is perfectly suited for the Substitution Method. Substitute ³/₉₅ Q for P in the demand function,

Now solve the equation for Q:

Either equation can be used to determine the corresponding value for P. If we substitute Q = 95 into the supply function, we get

The equilibrium price of $3 per gallon corresponds to a quantity of 95 thousand gallons of milk. At this price, suppliers are willing to supply 95 thousand gallons of milk and consumers are willing to buy 95 thousand gallons of milk.

---

 

We can also locate this equilibrium point using the Elimination Method.

Example 6    Use the Elimination Method to Find the Equilibrium Point

The demand and supply functions for the dairy industry are described by

Use the Elimination Method to find the equilibrium point for this system of equations.

Solution To use the Elimination Method, we must place all of the variables on one side of the equation and the constants on the other side.

This gives the equivalent system

The leading coefficient of the first equation is a 1, so we proceed to eliminating P from the second equation. To do this, multiply the first equation by -1 and add it to the second equation:

The fraction in the sum may look a bit strange, but it comes from converting the decimal to a fraction and adding the fractions:

Replace the second equation with the new second equation to obtain an equivalent system of equations:

Multiply the second equation by the reciprocal of ⁷⁷⁵/₉₅₀₀ to make the leading coefficient a 1,

This helps us to write the system of equations as

To eliminate Q from the first equation, multiply the second equation by ³/₉₅ and add it to the first equation:

Replace the first equation with this sum to yield the solution . This tells us that the equilibrium point is at 95,000 gallons of milk and a price of $3 per gallon.

---

 

The equilibrium point is at the same values when we solve the system of equations by the Substitution Method or the Elimination Method. In general, you’ll solve for the equilibrium point with only one of these methods.

We have looked at several examples of setting up a system of equations from an application and then solving the resulting system. We have broken the process up into several parts and illustrated each part individually to make them easier to understand. In reality, problems are usually not all that tidy. In the following example we’ll solve a problem involving a system of equations in two variables. Our strategy for doing this is fairly straightforward.

 

Example 7    Mixing Ethanol Blends

Flex fuel vehicles are designed to operate on a gasoline-ethanol mixture. This gasoline-ethanol mixture is called E85 and is 85% ethanol and 15% gasoline. Flex fuel vehicles perform almost identically to gasoline powered vehicles. Since E85 is less expensive than gasoline, it would appear that that flex fuel vehicles would be the wave of the future. However, the energy content of E85 is less than that of gasoline so flex fuel vehicles get worse mileage than gasoline powered vehicles. In general, the higher the percentage of ethanol in the fuel, the worse the mileage is.

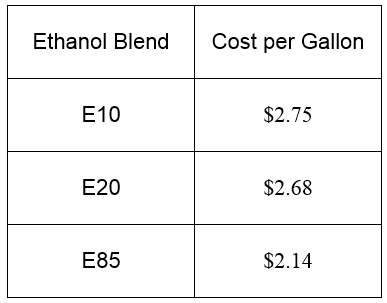
A recent study determined that several vehicles designed to run on gasoline are able to run well on gasoline-ethanol blends. In tests using E10 (10% ethanol), E20 (20% ethanol) and E30 (30% ethanol), the cost per mile traveled by vehicles using the three blends was lowest for vehicles using E20 or E30. Because of these results, gasoline stations around the country are beginning to sell several blends of ethanol to cash in on this result. A gasoline station in Rapid City, South Dakota carries three blends, E10, E20, and E85. The cost per gallon of each of these fuels is shown in the table below.

A customer wants to purchase 10 gallons of E20. The customer could simply purchase the 10 gallons at $2.68 per gallon. Or the customer could blend their own E20 using the available E10 and E85. How many gallons of E10 and E85 would the customer need to blend in their 10 gallon tank to effectively have E20? Would it be cheaper to blend E10 and E85 or to simply pump E20?

Solution In this problem, we need to compare the cost of pumping 10 gallons of straight E20 to the cost of a specific combination of E10 and E85 that will yield 20% ethanol.

It is straightforward to calculate cost of each type of fuel,

cost = ( cost per gallon ) ( number of gallons )

For instance, 10 gallons of E20 would cost

The key question is to determine if a blend of E10 and E85 would be cheaper. How much of each type of fuel would be needed to fill the tank and result in a mixture that is 20% ethanol? We’ll start with two variables, one to represent the amount E10 in gallons and another to represent the amount of E85 in gallons:

E10: amount of 10% ethanol fuel in gallons

E85: amount of 85% ethanol fuel in gallons

Writing out this description is key to our strategy. Not only does it help you to focus on what the unknowns are, but it also includes the units, gallons.

The problem includes copious amounts of information. However two pieces of information relate to the variables. First of all, the customer needs to fill a 10 gallon tank with a combination of two fuels. Since the variables represent the individual amount of fuels, the sum of the variables corresponds to the total amount of fuel,

The second important piece of information is that the mixture of fuel must contain 20% ethanol. For a 10 gallon tank, the amount of ethanol is 20% of 10 gallons or ( 0.20 )( 10 gallons ) = 2 gallons. This ethanol will come from the E10 which is 10% ethanol and the E85 which is 85% ethanol. By multiplying the percent times the gallons of fuel, we can determine how much ethanol is in the fuel. For instance 8 gallons of E85 and 2 gallons of E10 would have

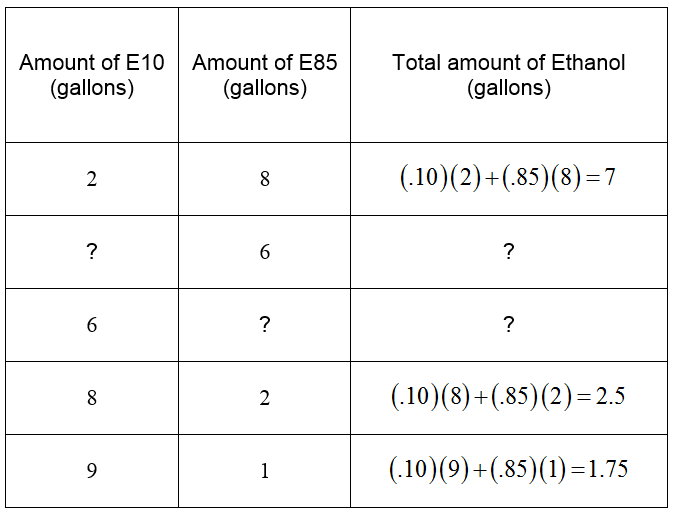
A mixture of 10 gallons of fuel with 7 gallons of ethanol would be a 70% mixture. This is clearly way too much ethanol. However, we could construct a table with differing amounts of fuel to help us determine the solution:

As the amount of E10 is increased and the amount of E85 is decreased, the total amount of ethanol in the mixture drops. Based on the table, the amount of E10 must be between 8 and 9 gallons and the amount of E85 must be between 1 and 2 gallons. It is unlikely that we could find the exact amounts of each type of fuel by expanding the table.

However, we can replace the amounts of fuel with variables that represent these amounts to give the equation

This gives us two equations in two variables that we can solve by the substitution method or the elimination method.

For this example, we’ll solve the system

Solve the first equation for E10 to yield E10 = 10 – E85. Substitute this expression into the second equation to obtain

Solve the equation for E85:

Now that we know that we’ll need ⁴/₃ gallon of E85, we can use the first equation to find the amount of E10:

Now let’s find the cost of this blend,

Compared to pumping 10 gallons of E20 (for a total of $26.80), pumping a blend of E10 and E85 (from the same pump!) saves about 11 cents.

How does this match the graph of each equation?

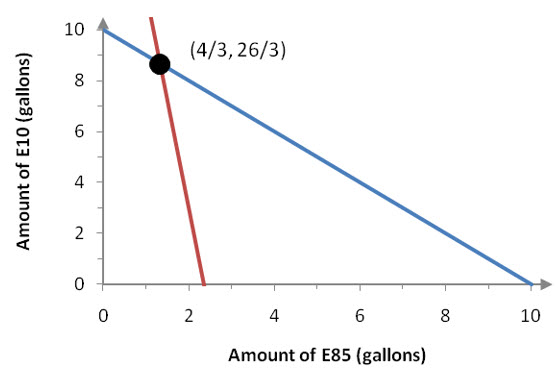
Figure 4 – By solving each equation for E10, we can graph E10 = 10 – E85 (blue) and E10 = 20 – 8.5 E85 (red) to see that the point of intersection is at the correct ordered pair.

Before moving on, we need to make sure the solution makes sense. In the table we created earlier, we noted that the amount of E10 had to between 8 and 9 gallons. Since ²⁶/₃ ≈ 8.67, our solution is consistent. The amount of E85  is 4/3 ≈ 1.33 which is between 1 and 2 as expected.

---

Review the steps we outlined for the strategy. Careful examination reveals that the solution above includes all six of the steps for solving an application.