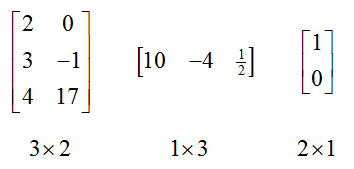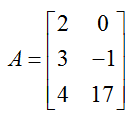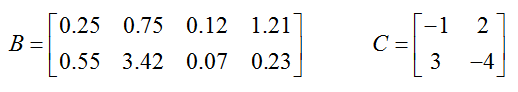What is a matrix?
A matrix is simply a table of numbers enclosed by a set of square brackets. These numbers may correspond to inventory levels, production quotas, or almost anything. We specify the size of a matrix by giving the number of rows and columns in the matrix.
An m x n matrix (read m by n) is a table of numbers with m rows and n columns enclosed by a set of square brackets.
The plural of matrix is matrices. The size of a matrix is always listed as row by column. Shown below are several matrices of various sizes.
Any matrix with only one row is also called a row matrix. The matrix in the center is an example of a row matrix. A matrix with only one column is called a column matrix. The matrix on the far right is an example of a column matrix.
Capital letters are used to name matrices. For instance, we might name the 3 x 2 matrix given above with the letter A,
The individual entries in the matrix are denoted by the corresponding lower case letter with a subscript. The number 4 in the third row and first column is called a31 and the number -1 in the second row and second column is called a22. In fact, we can match any entry to its name using the lowercase letter matching its name with a subscript. In general, amn is the entry in the mth row and nth column.
Example 1 Find the Matrix Entry
For the matrices
find the entries indicated in each part.
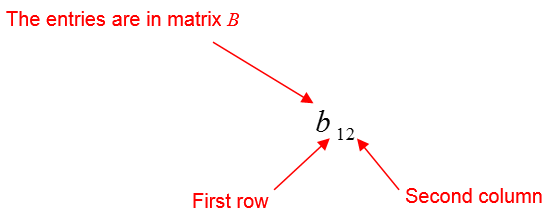
a. b12
Solution Let’s examine the matrix entry in detail.
The entry in the first row and second column of the matrix B is 0.75.
b. c21
Solution The entry in the second row and first column of C is 3.
c. b31
Solution This entry matches with the number in the third row and second column of B. Since B only has two rows, does not exist for the given matrix B.