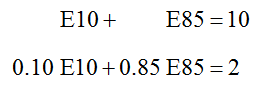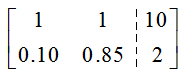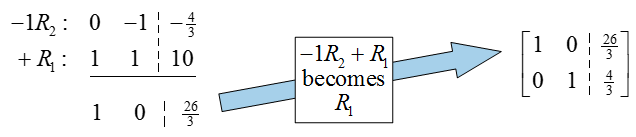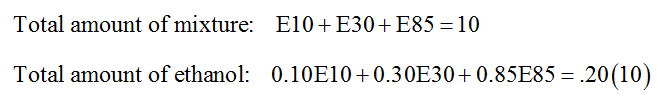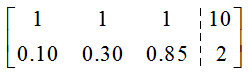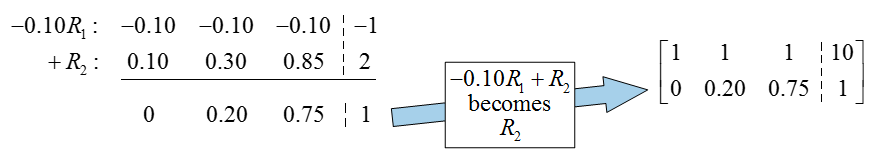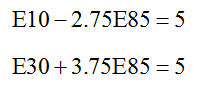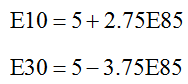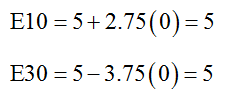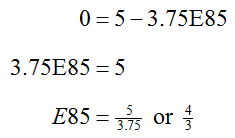How do you mix different grades of ethanol to create a new grade of ethanol?
In the next example we examine how to use matrices to solve the ethanol mixing problem from Section 2.2 and extend the example to more types of ethanol.
Example 9 Mixing Ethanol Blends
In Example 12 of section 2.2 we created a system of equations to describe a mix of E10 and E85 ethanol,
where E10 is the amount of 10% ethanol pumped in gallons and E85 is the amount of 85% ethanol pumped in gallons. The first equation describes the total amount in the mixture, 10 gallons. The second equation describes the total amount of ethanol in the mixture, 20% of 10 gallons or 2 gallons.
Solve this system of equations by finding the reduced row echelon form for the augmented matrix.
Solution The augmented matrix for this system is
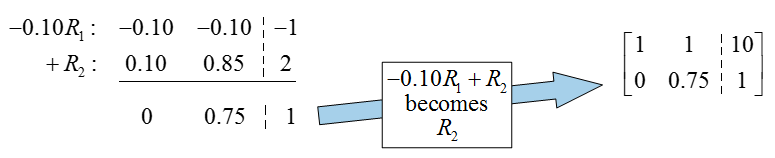
where the first column corresponds to E10 and the second column corresponds to E85. To convert this matrix to reduced row echelon form, we must create pivots in the first and second columns and put zeros above and below the pivots. There is already a 1 in the first row and column, so we need to use row operations to put a 0 below it:
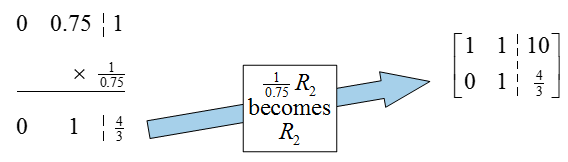
We can place a pivot in the second row and column by multiplying the row by the reciprocal of 0.75,
A 0 is placed above the pivot in the second column by multiplying the second row by -1, adding it to the first row, and putting the result in the first row:
Based on this reduced row echelon form, E10 = 26/3 and E85 = 4/3. This means that mixing 26/3 gallons of 10% ethanol with 4/3 gallons of 85% ethanol will yield 10 gallons of 20% ethanol.
Example 10 Mixing Three Types of Ethanol
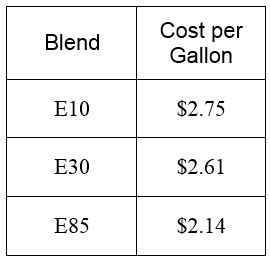
In some Midwestern states, three different blends of ethanol are available. E10 contains 10% ethanol, E30 contains 30% ethanol, and E85 contains 85% ethanol. How much of each of the blends must be mixed to make 10 gallons of 20% ethanol? If the price per gallon for each type is given in the table below, what is the least that the 10 gallon blend would cost?
Solution This problem adds another type of ethanol that should contribute to the total number of gallons in the mixture and the total amount of ethanol in the mixture. Each of the two equations in Example 9 needs another term corresponding to E30:
where E10 is the number of gallons of 10% ethanol, E30 is the number of gallons of 30% ethanol, and E85 is the number of gallons of 85% ethanol.
The augmented matrix for this system is
As in the previous example, the pivot in the first column is already in place so we simply need to use row operations to put a 0 below it:
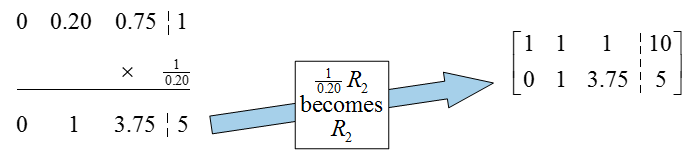
To put a pivot in the second column, multiply the second row by the reciprocal of 0.20:
To put a 0 above the pivot,
Writing this matrix as an a system of equations leads to
E85 appears in both equations so we’ll solve for the other variables in terms of E85,
This system has many solutions, but we must be careful. These variables represent gallons of different ethanol blends. Because of this, the variables cannot be negative. As long we pick reasonable values for E85, we can insure that all the variables are nonnegative. For instance, if we set E85 = 0 we get
This solution makes sense since mixing equal amounts of E10 and E30 should yield a mixture with a percent ethanol midway between 10% and 30%.
Notice that as we increase the amount of E85, the amount of E10 increases (the E85 term is added in the E10 equation) and the amount of E30 decreases (the E85 term is subtracted in the E30 equation). Eventually the amount of E30 will equal 0 as E85 is increased. This occurs when
Reasonable values for E85 are from 0 to 4/3 including 0 and 4/3 since this leads to non-negative values for E10 and E30 as well.
We can calculate the total cost of any combination using cost per gallon of each type of ethanol. For instance, 5 gallons of E10 and 5 gallons of E30 would cost
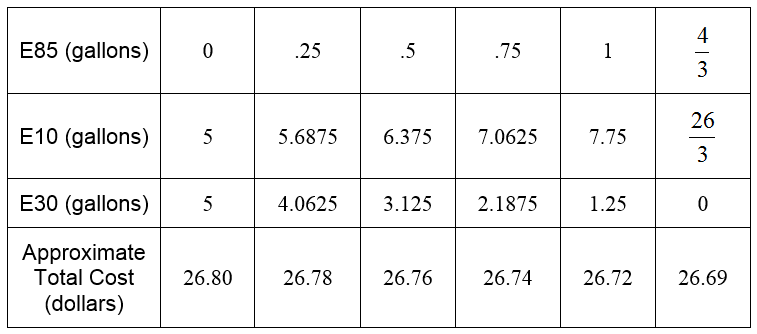
Here is a table of some of the possible solutions based on
and their corresponding total costs:
As the amount of E85 is increased, the total cost drops. Each increase of 0.25 gallons of E85 leads to a drop in the total cost of about 0.02 dollars. The lowest cost appears to come from mixing 4/3 gallons of E85 and 26/3 gallons of E10. Using any more E85 would require us to use a negative amount of E30. Even though this would yield a lower cost, it is not a reasonable value for this problem.