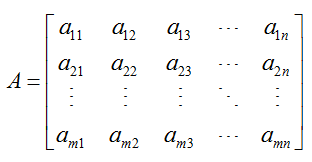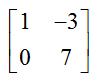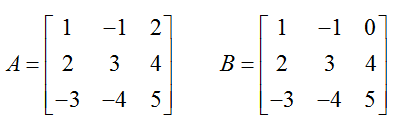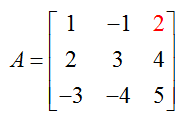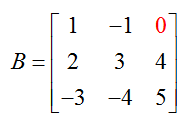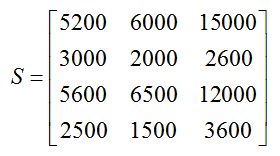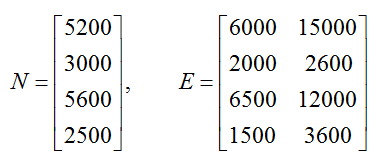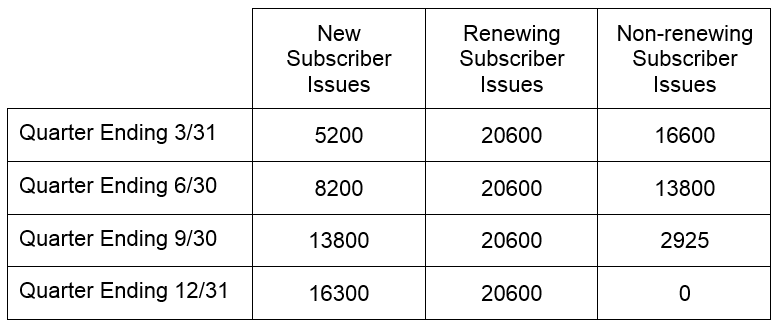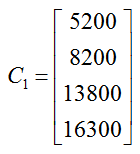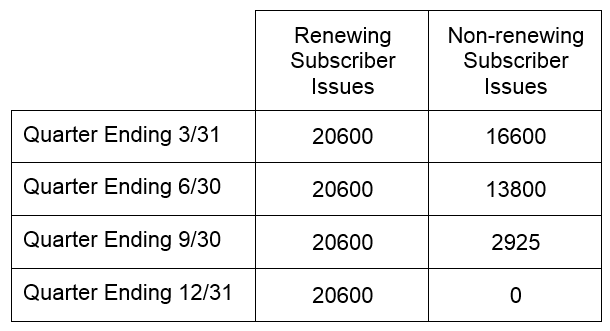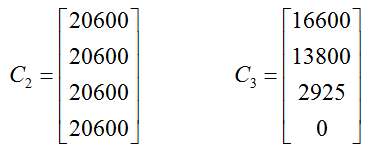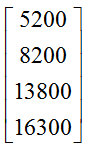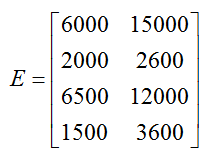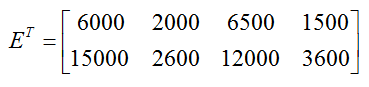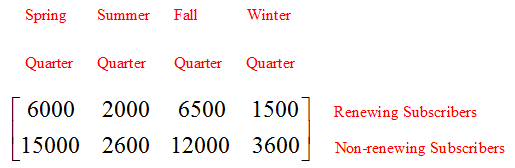How is information organized in a matrix?
When we use a matrix to organize data, all of the definitions we developed in Chapter 2 still apply. You’ll recall that a matrix can have any number of rows and columns and is typically named with a capital letter. A matrix with m rows and n columns named A would look like
Notice that this matrix does not contain a dashed vertical line in front of the last column. The dashed line is unique to augmented matrices and is used to separate the coefficients from the constants. The dots in the matrix indicated a pattern in the matrix. In this case, the dots indicate the arbitrary number of rows m and columns n in the matrix.
The individual entries (also called elements) of the matrix are symbolized with lowercase letters, like amn, and these symbols represent numbers. The subscript on the lowercase letter indicates the location of the entry in the matrix. The symbol a23 represents the number in the second row, third column of the matrix.
The size of a matrix (also called the dimensions of the matrix) is the number of rows and columns in a matrix. For the matrix A with m rows and n columns, we would say the size of the matrix is m x n (read m by n).
Several sizes of matrices are given special names. A matrix with the same number of rows and column is called a square matrix. An example of a square matrix is the 2 x 2 matrix
The exact number of rows and columns in a square matrix is not important, only the fact that the number of rows and columns is the same.
Matrices with a single row or a single column are also given special names. Row matrices like or
are matrices with only a single row, but any number of columns. Column matrices like


The size of a matrix is an important prerequisite in determining if two matrices are equal.
Two matrices are equal if they have the same size and each entry in one matrix is equal to the corresponding entry in the other matrix.
Example 1 Matrix Terminology
The matrices
are 3 x 3 square matrices.
a. What is the value of the entry b32?
Solution The subscript on b32 refers to the entry in the third row, second column of the matrix B. Therefore, b32 = -4.
b. Is a23 = b23?
Solution The subscripts on a23 and b23 refer to the corresponding entries in the second row, third column of A and B. Since the entry in that location is 4 in both matrices, a23 = b23 and is equal to 4.
c. Is A = B?
Solution For the matrices to be equal, they must have the same size and each entry in A must be equal to the corresponding entry in B. Both matrices are 3 x 3. In part b, we determined that the entries in the second row, third column of each matrix were equal. However, a13 in
and b13 in
are not the same so A ≠ B. This is in spite of the fact that every other set of corresponding entries are equal.
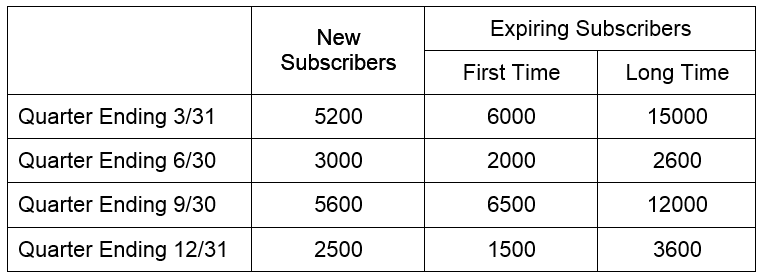
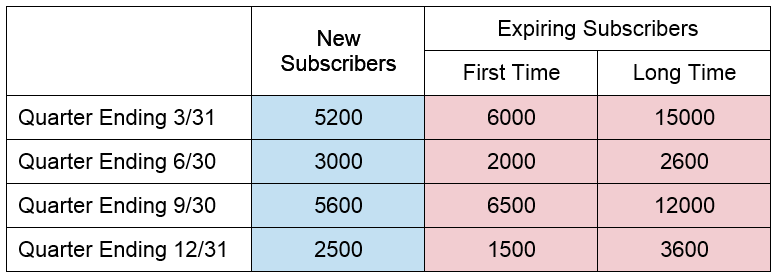
Ed Magazine is a fictional magazine that publishes four issues each year. It has a loyal base of subscribers and twice a year it conducts subscription drives for new subscribers. At the same time they are acquiring new subscribers, the current subscriber’s subscriptions are expiring. Some of these expiring subscriptions belong to first time subscribers and others are long time subscribers who have renewed their subscriptions in the past. The table below shows the numbers of new and expiring subscribers by quarter.
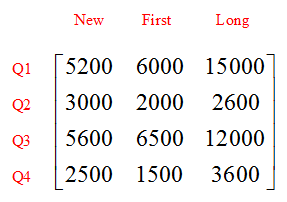
Although this information could be placed in a matrix in several different ways, two approaches stand out. Since the rows in the table correspond to the four different quarters during the year and the columns correspond to numbers of subscribers, we could use a matrix with four rows and three columns:
Normally we don’t include the red labels on a matrix. However, they are often included to help clarify how the information in the matrix is organized. To name this matrix of subscribers, we could use the letter S and write
This organization capitalizes on the fact that all of the numbers in the table indicate the number of subscribers in a certain category.
Let’s look at the table differently.
The rows in the table still refer to quarters, but now the shading in the table emphasizes a difference in the numbers. The numbers in the blue region corresponds to the number of new subscribers by quarter and the red region corresponds to subscribers whose subscriptions are expiring.
With this difference in mind, we could define two matrices for this table,
The matrix N is a 4 x 1 column matrix representing the number of new subscribers of Ed Magazine. The matrix E is a 4 x 2 matrix representing the number of expiring subscribers in two categories by quarter. Depending on the application, these matrices may be more useful than the 4 x 3 matrix S.
Example 2 Organize Information in a Matrix
A magazine’s circulation is the number of issues it distributes. Ed Magazine is distributed to three categories of subscribers each quarter.
Use this information to define three matrices named C1, C2, and C3, where C1 describes the number of issues distributed to new subscribers, C2 describes the number of issues distributed to subscribers who have renewed their subscription, and C3 describes the number of issues distributed to subscribers who have not renewed their subscriptions.
Solution The first column in the table corresponds to issues distributed to new subscribers
If we let the rows in the matrix C1 correspond to the quarters, then can organize the information in the table in a 4 x 1 matrix as
Alternatively, we could also let the quarters correspond to the columns in a 1 x 4 matrix and define
Either matrix organizes the information appropriately. Since the original table matches each row with a quarter, we’ll follow the same principal and let the rows of the matrices correspond to the quarters.
Letting the rows match the quarters, the other columns in the table give the entries in C2 and C3,
In Example 2, we mentioned the fact that the data in the first column of the table could be written as a row matrix or a column matrix. These matrices are examples of transposes. In other words, the matrix
is the transpose of the matrix
Example 3 Find the Transpose of a Matrix
Find and label the transpose of the expiring subscriber matrix
Solution To get the transpose of the expiring subscriber matrix, we interchange the rows and columns. In other words, the columns of E become the rows of the transpose ET or the rows of E become the columns of the transpose ET to yield
In the original matrix E, the rows of the subscriber matrix correspond to the quarters and the columns tell us the subscriber category.
In the transpose, these roles are reversed.
The information in each matrix is the same, but organized differently.