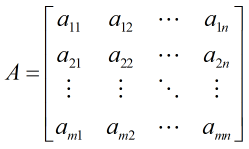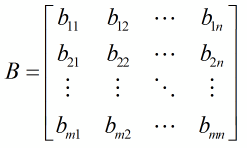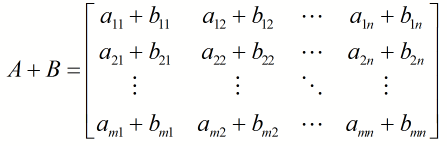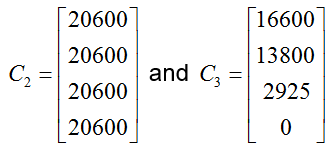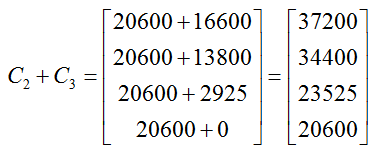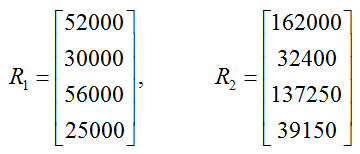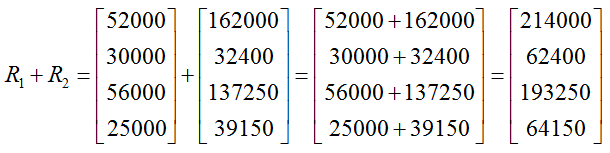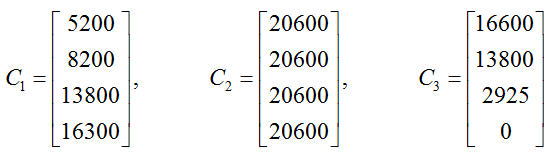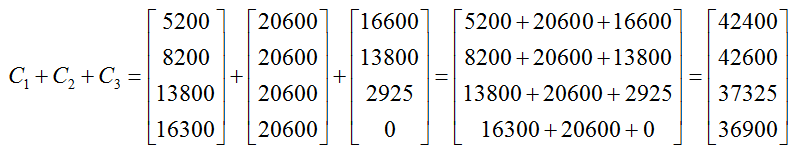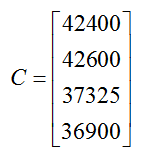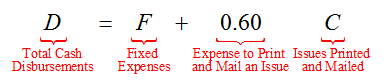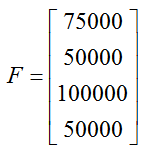How do you add matrices?
The sum of two matrices is accomplished by adding the corresponding entries in the matrix. Because of this, the matrices being added must have the same size.
The circulation matrices
indicate the quarterly circulation of Ed Magazine for renewing and non-renewing subscribers. The sum of these matrices,
is found by adding the corresponding entries in each matrix. This sum shows the total circulation for these two subscriber groups together. For instance, the entry in the second row tells us that 34,400 issues were produced and sent to renewing and non-renewing subscribers in the second quarter.
Example 5 Add Two Matrices
The cash receipts from subscribers for Ed Magazine are
Find and interpret the sum R = R1 + R2.
Solution Each matrix is a 4 x 1 matrix so it is possible to calculate the sum. The sum is found by adding the corresponding entries,
To discover what the entries in the sum represent, let’s look at the second row. It is calculate from the entries in the second row of R1 and R2,
Since the magazine receives money from new subscribers or renewing subscribers, the sum is the total cash receipts from all subscribers. This particular sum comes from the row corresponding to the second quarter. Other rows give the total cash receipts from subscribers for other quarters.
The sum of several matrices is carried out in a similar fashion. As long as each matrix in the sum has the same size, the entries in the sum are calculated by adding the corresponding entries of each matrix.
Example 6 Add Several Matrices
The circulation for Ed Magazine is broken into three matrices: the circulation for new subscribers C1, the circulation for subscribers who renew their subscription C2, and the circulation for subscribers who do not renew their subscription C3. When organized into matrices, this information becomes
Find and interpret C = C1 + C2 + C3.
Solution We can find the sum of three matrices as long as each matrix has the same size. Since each matrix in this sum is 4 x 1, the sum of these three matrices is found by adding the corresponding entries of each matrix:
Each row of the sum gives the total circulation in the corresponding quarter. For instance, in the spring quarter Ed Magazine produced 42400 issues of the magazine.
Example 7 Matrix Arithmetic
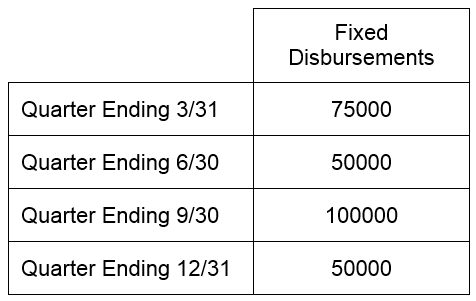
Ed Magazine maintains production, editorial and advertising staff that help publish the magazine each quarter. These disbursements do not change even if the number of issues produced increases. Because these disbursements are fixed, they are called fixed disbursements. The table below gives these disbursements for each quarter.
Recall that the magazine pays $0.60 to print and mail each issue. In Example 6, we found that the total circulation by quarter is given by the matrix
Write the fixed disbursements in a matrix F and use it to find a matrix for the total cash disbursements
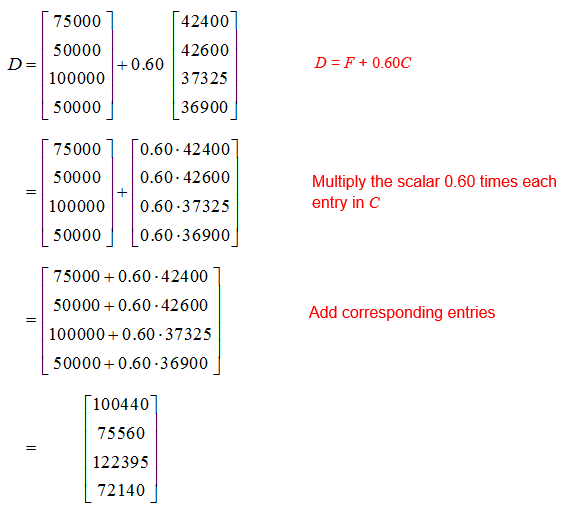
Solution The circulation matrix gives the number of issues printed and mailed each quarter. If we multiply this matrix C by the expense to print and mail each issue, the product tells us how much is being spent to print and mail the magazine each quarter. The total cash disbursements D are calculated by adding the fixed disbursements in each quarter, F, to the expense of printing and mailing the magazine in each quarter.
We summarize this relationship by writing
The second term gets larger as more magazines are printed and mailed so it is referred to as the variable expenses. Since the circulation matrix C is a 4 x 1 matrix with the rows corresponding to quarters, the fixed disbursements F must also be a 4 x 1 matrix. This insures that we’ll be able to carry out the sum of F and 0.60 C.
The fixed disbursements in the table yield the matrix
With these matrices, the total cash disbursements are
Each entry in D gives the total cash spent by Ed Magazine on fixed expenses and the variables expenses in a particular quarter. These disbursements vary by quarter since different issues may require more or less production and editing and the circulation changes throughout the year.