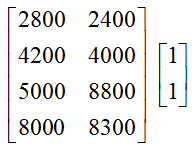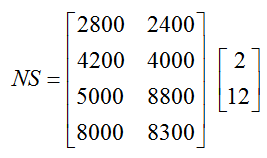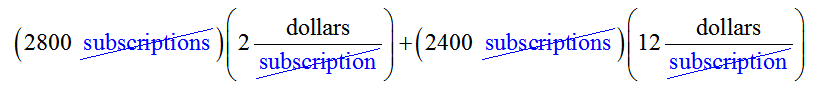How do you interpret the entries in a product of two matrices?
Befre attempting to compute or interpret what the product tells you, it is instructive to determine the size of the product. As indicated earlier, the product of an m x k matrix and a k x n matrix is an m x n matrix. Once we know the size of the product, we can compute each of the entries in the product. The entries in the product are formed by corresponding the rows and columns in the factors, multiplying the entries, and summing the results. This operation is often very useful in computing various quantities in business. However, it is often not obvious exactly what the product tells you.
In a typical application, we can use the labels on the number of rows m in the first matrix to label the rows of the product. To label the columns in the product, write out the calculation for the first entry with the units on each factor. By analyzing the units, we can deduce what that entry tells us. The other entries will have a similar interpretation to the first entry.
Example 3 Interpret the Product of Two Matrices
The number of new subscriptions by quarter is given by the matrix
New subscriptions may come from a subscription service or may come from the magazine’s marketing. The columns of N indicate the number of subscriptions from each source.
Find and interpret the product
Solution In this product we are multiplying a 4 x 2 matrix times a 2 x 1 matrix. Since the number of columns (2) in the first matrix matches the number of rows in the second matrix (2), we can carry out the matrix multiplication. The resulting product will be a 4 x 1 matrix:
Notice that each entry in the product is simply the sum of the entries on the same row in the first matrix. Since these values are the number of new subscriptions in that quarter, the sum in the product corresponds to the total number of new subscriptions in that quarter.
For instance, in the first quarter a total of 5200 new subscriptions were received from the subscription service and the magazine’s marketing efforts,
The numbers in the second matrix have no units. The effect of multiplying by the matrix is to add the entries in each row of the matrix N.
Example 4 Interpret the Product of Two Matrices
The new subscriptions described by the matrix
contribute different amounts of cash to Ed Magazine. Subscriptions enlisted by the subscription service pay $10 for a subscription, but only $2 goes to the magazine. Subscriptions developed through the magazine’s marketing campaigns pay $12 and all of this cash goes to the magazine. We can summarize this information in the matrix
Find and interpret
Solution Let’s check the size of each matrix to insure that the matrix multiplication is possible.
The number of columns in N representing the number of new subscriptions and the number of rows in S representing the cash from subscriptions are both equal to 2 so the multiplication can be carried out to give a 4 x 1 product.
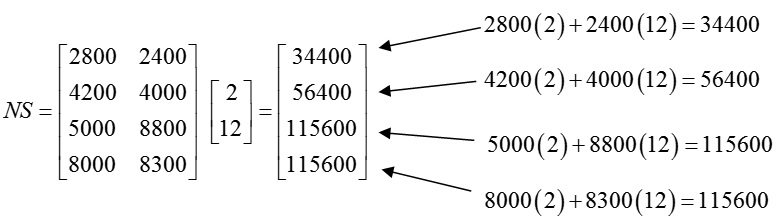
We can form the entries in the product by corresponding the rows in N with the column in S:
The four rows in the product correspond to the four quarters, but what do the entries tell us about those quarters?
To answer this question, let’s look at the first entry in detail:
Each term has units of dollars and indicates the amount of cash received from the sales of subscriptions to new subscribers of each type (from the subscription service and from the magazine’s promotions). So the sum, 34400 dollars, represents the total amount of cash received from both types of subscribers together.
Other entries can be analyzed similarly to show the total cash received from new subscribers in the other three quarters.