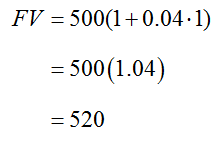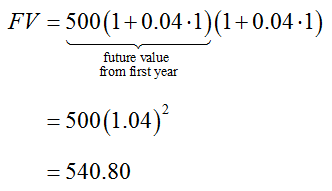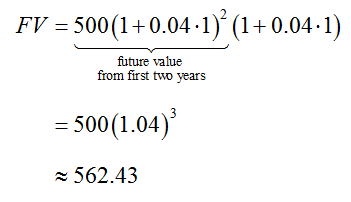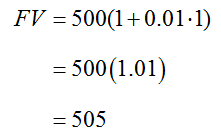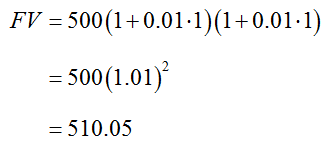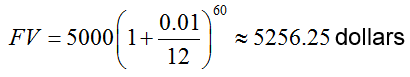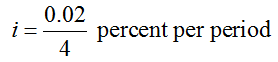What is compound interest?
In a loan or investment earning compound interest, interest is periodically added to the present value. This additional amount earns interest. In other words, the interest earns interest.
Let us illustrate this process with a concrete example. Suppose we deposit $500 in an account that earns interest at a rate of 4% compounded annually. This rate is the nominal or stated rate. By saying that interest is compounding annually, we mean that interest is added to the principal at the end of each year.
For instance, we use the simple interest formula, FV = PV (1 + rt), to compute the future value at the end of the first year,
To find the future value at the end of the second year, we let the present value be the future value from the end of the first year in the simple interest formula,
Since the present value in this amount includes the interest from the first year, the interest from the first year is earning interest. This is the effect of compounding.
To find the future value at the end of the third year, we let the future value at the end of the second year be the present value in the simple interest formula,
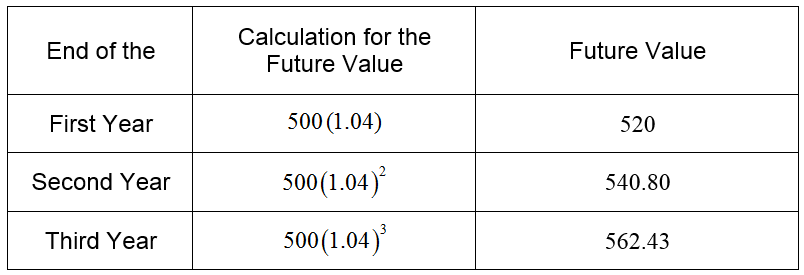
Let us summarize these amounts in a table.
The middle column establishes a simple pattern. At the end of each year, the future value is equal to the present value times several factors of 1.04. These factors correspond to the compounding of interest.
In general, if interest is compounded annually, then the future value is
where PV is the principal, r is the nominal rate and t is the time in years.
If interests compounds more than once a year, finding the future value is more challenging. It is more likely that interest is compounded quarterly (4 times a year), monthly (12 times a year) or daily (365 times a year). The length of time between which interest is earned is the conversion period. The length of time over which the loan or investment earns interest is the term. To account for compounding over shorter conversion periods, we need more factors in the expression for the future value. However, in each of these factors we only earn a fraction of the interest rate.
For instance, suppose deposit $500 in an account earning 4% compounded quarterly. To calculate the future value, we multiply the principal by a factor corresponding to one-fourth of the interest rate each quarter. The future value after one quarter is
After two quarters, the future value contains two factors corresponding to one percent interest per quarter,
Continue this pattern for twelve conversion periods (twelve quarters or three years) gives
If we compare this expression to the expression for compounding quarterly, FV = 500(1.04)3, we note several differences. When we compound quarterly, we get four times as many factors in the future value. This is due to the fact compounding quarterly means we need four times as many factors. When we compound quarterly, each factor utilizes a rate that is one-fourth the rate for compounding annually.
Compound Interest
The future value FV of the present value PV compounded over n conversion periods at an interest rate of i per period is
where
and
You may also see compound interest computed from the formula This is the exact same formula as the one above except the present value is called the principal P and the future value is called the accumulated amount A.
Example 1 Compound Interest
A customer deposits $5000 in an account that earns 1% annual interest compounded monthly. If the customer makes no further deposits or withdrawals from the account, how much will be in the account in five years?
Solution To utilize the compound interest formula, FV = PV (1 + i)n, we must find the present value PV, the interest rate per conversion period i, and the number of conversion periods n. The present value or principal is the amount of the original deposit so . The account earns 1% annual interest, compounded monthly. This means the account earns
over each conversion period. Since the interest is compounded monthly over 5 years, there are n = 12 · 5 or 60 conversion periods during the time this money is deposited. The future value is
If the future value, interest rate, and number of conversion periods is known, we can solve for the present value in FV = PV (1 + i)n. In problems like this, we want to know what amount should we start with to grow to a known future value.
Example 4 Present Value
A couple needs $25,000 for a large purchase in five years. How much must be deposited now in an account earning 2% annual interest compounded quarterly to accumulate this amount? Assume no further deposits or withdrawals during this time period.
Solution To find the amount needed today, we must find the present value of $25,000. The interest for each conversion period is
The account earns interest over a total of 4·5 or 20 conversion periods. Substitute these values into the compound interest formula, FV = PV (1 + i)n, and solve for PV:
We round the present value in the last step to two decimal places. This ensures the value is accurate to the nearest cent. If the couple invests $22,626.57 for five years, it will grow to $25,000 at this interest rate.