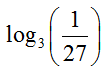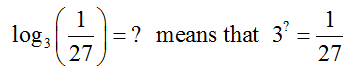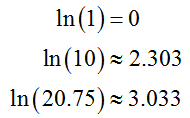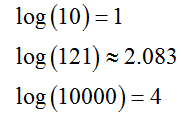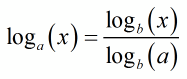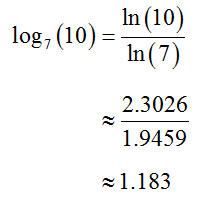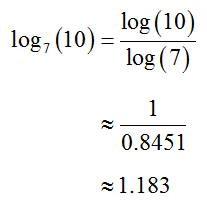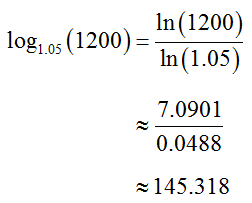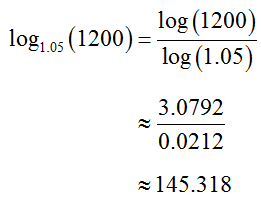Section 5.2 Question 2

How do you evaluate a logarithm?

Many logarithms may be calculated by converting them to exponential form. Suppose we want to calculate the value of log₂(16). Start by writing this expression as a logarithmic form,

 We could write the output with a variable, but a question mark suffices to indicate what we want to find. If we convert this form to an exponential form with a base of 2,

The left hand side may be written with the base 2 as 2⁴. Substitute this expression in place of 16,

Since the exponent on the left side must be 4, this is also the value in the original exponential form,

This strategy works well as long as we can write the number on the right with the same base as the exponential on the other side of the equation.

Example 4         Evaluate the Logarithm

Find the value of each logarithm by converting to exponential form.

a.  

Solution Write the logarithm in logarithmic form and convert to exponential form,

Since the value of the logarithm is 2,

b.   

Solution The logarithmic and exponential forms are

Since  the value of the logarithm is -3, The negative power makes the reciprocal.

c.   

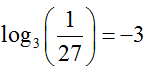
Solution The logarithmic and exponential forms are

The value of the logarithm is 2, In effect, the number 2 is put into the base of e and the natural logarithm reverses this process.

---

Not every logarithm may be solved by converting to exponential form. For this strategy to work, we must be able to write each side of the exponential form with the same base.

Scientific and graphing calculators are both able to calculate natural logarithms and common logarithms. Natural logarithms are calculated using a button labeled something like LN. Using this button, you should be able to do the following calculations by pressing the LN button, entering the number, and pressing the ENTER or = button.

You may also calculate common logarithms in a similar manner using a button that is typically labeled LOG. Using this button, you should be able to compute each of the following common logarithms.

Using these buttons, you can compute any natural or common log. Even the logs that may not be solved by converting to exponential form may be computed on a calculator. Some calculator may even have a button for calculating a logarithm with any positive base. To see if your calculator is able to do this, consult the manual for your calculator. If your calculator does not have this button, you can use the change of base formula to compute logarithms with any positive base.

This formula is used to compute a logarithm with base a by converting it to two logarithms with base b. The base b can be any positive number not equal to 1, but usually it is a base of 10 or e so that a calculator may be used to compute the right hand side of the formula.

Example 5         Compute the Logarithm

Find the value of each logarithm using the Change of Base formula for Logarithms.

a.  

Solution We may use the Change of Base formula to convert this logarithm to natural logarithms or common logarithms. If we convert to natural logarithms we get

A calculator is used to evaluate the natural logarithms. The values of the individual logarithms are shown above, but it is a good  idea to type the entire expression. This avoids rounding in the middle of the problem and then rounding again at the end. Ideally you should only round once.

If we convert to common logarithms,

The value of the original base 7 logarithm is the same whether it is computed from natural logs or common logs.

b.  

Solution Use the Change of Base formula with natural logarithms to give

You may also calculate the value using common logarithms,