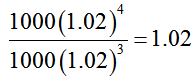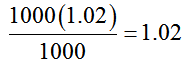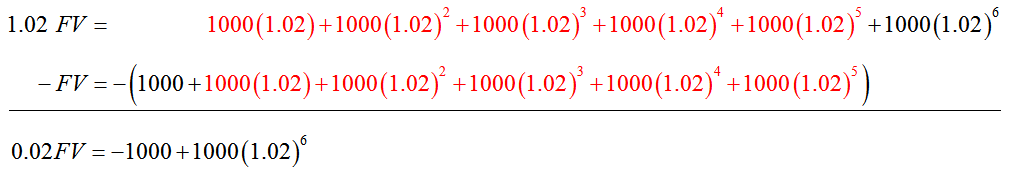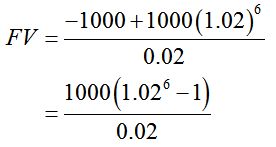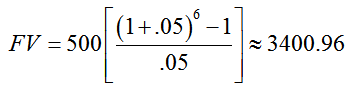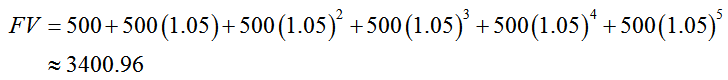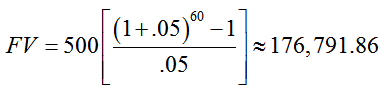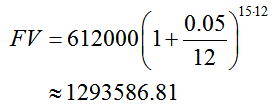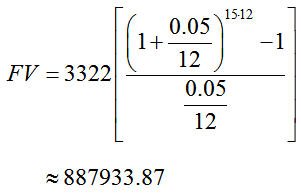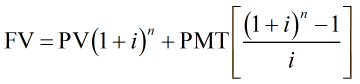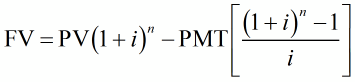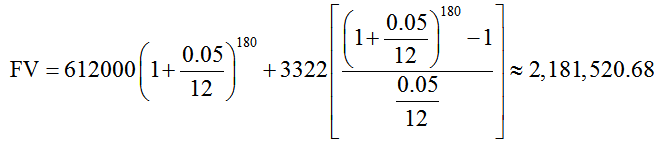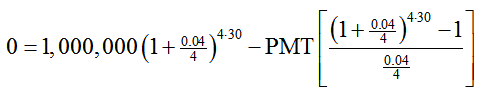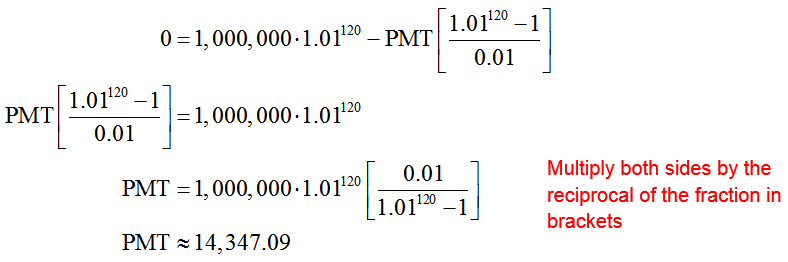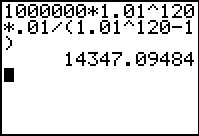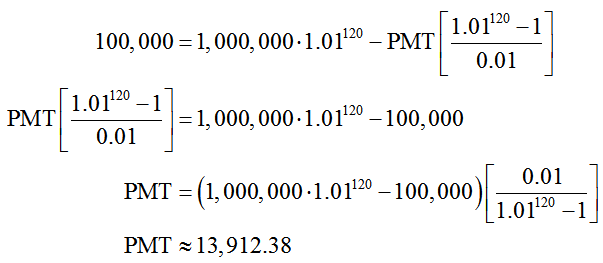What is an ordinary annuity?
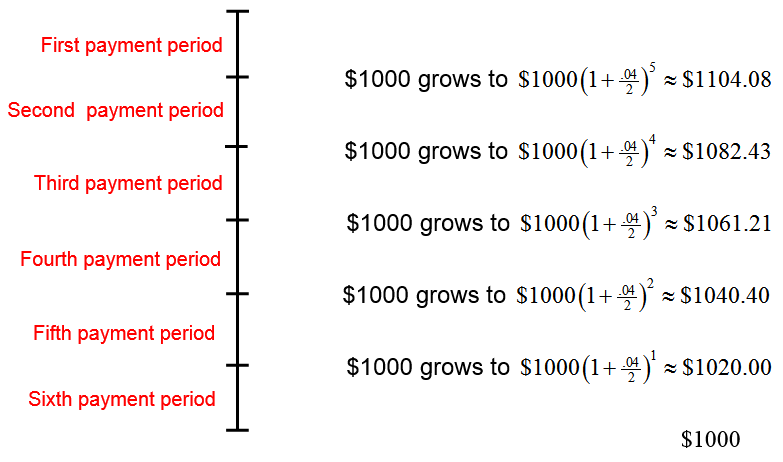
Let’s look at an ordinary annuity that is certain and simple. By this, we mean an annuity over a fixed term whose payment period matches the interest conversion period. Additionally, the payments to the annuity are made at the end of the payment period. Suppose a payment of $1000 is made semiannually to the annuity over a term of three years. If the annuity earns 4% per year compounded semiannually, the payment made at the end of the first six-month period will accumulate
This means $1000 is multiplied by 1.02 five times, once for each of the remaining six-month periods.
The next payment also earns interest, but over 4 six-month periods. This payment has a future value of
This process continues until we have the future value for each payment.
The last payment occurs at the end of the last period and earns no interest. Examining each expression for the future value, it appears that there is a pattern to the individual future values. Each future value forms a number corresponding to a geometric sequence.
A geometric sequence is an infinite list of numbers with the form
The amounts above correspond to the first six numbers in the geometric sequence
In this case, a = 1000 and r = 1.02. The numbers in the geometric sequence are called terms. For this geometric sequence, we can number the terms to make them easy to refer to.
In this geometric sequence, each term is 1.02 times larger than the term before it. In fact, the ratio of any two adjacent terms is 1.02. For instance, the ratio of the fourth and fifth terms is
Similarly, the ratio of the first and second terms is
In a geometric series, dividing a term by the preceding one should results in the same number. This number is called the common ratio for the geometric sequence and corresponds to r.
Notice that the power on the 1.02 factor is one less than the term number. This pattern holds in general and leads us to the following pattern.
For any n ≥ 1, the nth term of a geometric sequence is a r n-1.
It might seem as though this general expression might not apply to the first term. In this case, n = 1, so the first term is 1000(1.02)0 or 1000. Other terms may be identified as long as the values for a, r, and n are known.
Example 1 Terms of a Geometric Sequence
Find the fourth and tenth terms of the geometric sequence with a first term 500 and r = 1.05.
Solution If the first term is 500, then a = 500. The fourth term (n = 4) in the geometric sequence is ar3 or 500(1.05)3. This is equal to 578.8125.
The tenth term is 500(1.05)9 ≈ 775.6641.
Let’s continue to look at the future value of a payment of $1000 made semiannually to an annuity over a term of three years. The future value of the annuity FV is the sum of the future values of each payment and corresponding interest is
This sum represents the future value of the annuity. For a sum with few terms, it is easy to add these amounts to give a future value of about $6308.12. This includes six payments of $1000 and interest of $308.12. We can find the same amount using an alternate strategy.
Start by multiplying both sides of the expression for the sum by 1.02 to yield
Subtract the sides of this equation and the previous equation:
Each equation contains identical terms that are highlighted in red. When those terms are subtracted, many terms drop out leaving us with
Each side of this equation may be divided by 0.02 and simplified to yield
This expression yields the same amount as adding the terms directly, $6308.12.
If the payments to the annuity increase in frequency or take place over a longer period of time, it is not convenient to add all of the terms directly. This strategy allows us to find the sum of any number of terms of a geometric sequence.
In the terms of the geometric sequence we have been examining, we can recognize the payment PMT and interest rate per period i. If the payments are paid at the end of n periods, the sum of the accumulated amount of each payment is
Using the strategy, this sum may be written in a simplified form.
Future Value of an Ordinary Annuity
If equal payments of PMT are made into an ordinary annuity for n periods at an interest rate of i per period, the future value of the annuity FV is
We use this expression to calculate the sum when there are any number of terms.
Example 2 Find the Future Value of the Annuity
An investor deposits $500 in a simple annuity at the end of each six-month payment period. This annuity earns 10% per year, compounded semiannually.
a. Find the future value if payments are made for three years.
Solution Find the future value of this ordinary annuity using 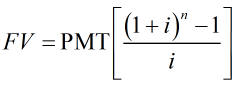
In this case, PMT = 500, i = 0.05, and n = 6. This gives
This is calculated in a TI Graphing Calculator as shown below.
We could also find this same amount by adding the terms directly,
The six payments of $500 have earned $3400.96 – $3000 or $400.96 in interest over the life of the annuity.
b. Find the future value if payments are made for 30 years.
Solution In this ordinary annuity, the term is much longer. The geometric series would have 30∙2 terms and it would not be practical to add the terms directly. However, if we set R = 500, i = 0.05, and n = 60 in the formula for the future value of an annuity, we get
This is calculated in a TI Graphing Calculator as shown below.
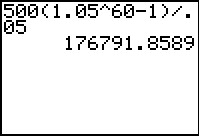
Solution Over the term of the annuity, sixty payments of $500 are made for a total of $30,000. This yields $176,791.86 – $30,000 or $146,791.86 in interest.
The future value of an ordinary annuity formula assumes that the annuity starts out with a balance of zero. However, the annuity may have an existing balance and the payments are added to that amount. In this case, the balance grows according to the compound interest formula. The payments grow according to the future value of the annuity. The sum of these amounts is the future value of both investments combined.
Example 3 Find the Future Value of a Retirement Account
An employee’s retirement account currently has a balance of $612,000. Suppose the employee contributes $3322 at the end of each month. If the account earns a return of 5% compounded monthly, what will the future value of the account in 15 years?
Solution The original balance grows according to the compound interest formula, . The original amount is PV = 612,000, the interest rate per period is
, and the number of periods over 15 years is n = 15 · 12.
This is calculated on a TI Graphing Calculator as shown below.
The future value of the payments into the annuity grow according to 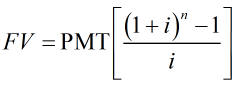
This is calculated on a TI Graphing Calculator as shown below.
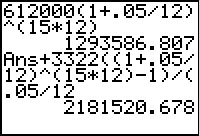
The sum of future value for the compounded amount and the future value of the annuity is $2,181,520.68.
We can combine the two amounts into a single formula that accounts for payments into an existing account that has some balance. In this context, the balance is called the present value. It corresponds to the value of the account at the time the payments commence.
Future Value of an Ordinary Annuity Whose Present Value Is Not Zero
If payments PMT are made to an ordinary annuity whose present value is PV, the future value is
If payments PMT are made from an ordinary annuity whose present value is PV, the future value is
We could have used the first formula to calculate the future value in Example 3,
We would calculate this amount on a TI Graphing Calculator in two steps.
In Examples 4, four of the five values in the future value formula for an ordinary annuity are known. This allows us to solve for the remaining value.
Example 4 Find the Payment from an Annuity
A savvy investor has accumulated $1,000,000 in an ordinary annuity. The annuity earns 4% interest compounded quarterly. She wishes to receive payments from the annuity each quarter for the next 30 years.
a. If the annuity will end up with no money in 30 years, what payment should she receive?
Solution Since the payments are made from an ordinary annuity, we’ll start from the future value of an ordinary annuity formula,
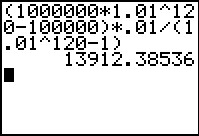
The annuity currently contains $1,000,000, so PV = 1,000,000. The investor wants the value of the annuity to be $0 in 30 years. This means FV = 0. Substitute these values, the interest rate per period , and the number of periods n = 4 · 30 to yield
To solve for the payment PMT, simplify and isolate the payment:
This is calculated in a TI Graphing Calculator as shown below.
The quarterly payment is $14,347.09.
The payment has been rounded down to insure all of the payments are equal. This will leave a small amount of money in the annuity at the end of 30 years. However, you could also round up if you realize the last payment might be different from the earlier payments.
b. The investor wishes to leave a balance in the annuity to leave to her heirs. If the annuity is to end contain $100,000 in 30 years, what payment should she receive?
Solution In this case, she wishes FV = 100,000. Change the future value to this amount an solve for the payment in
This is calculated in a TI Graphing Calculator as shown below.
Reducing the payment by $434.71 insures that the annuity will contain $100,000 in 30 years.