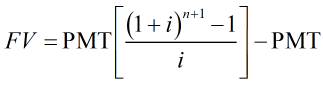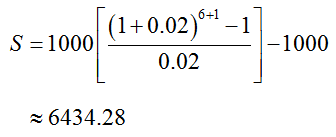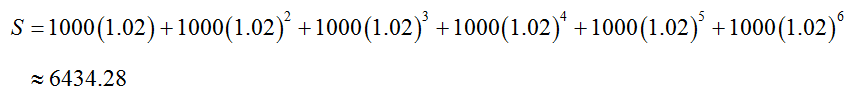What is an annuity due?
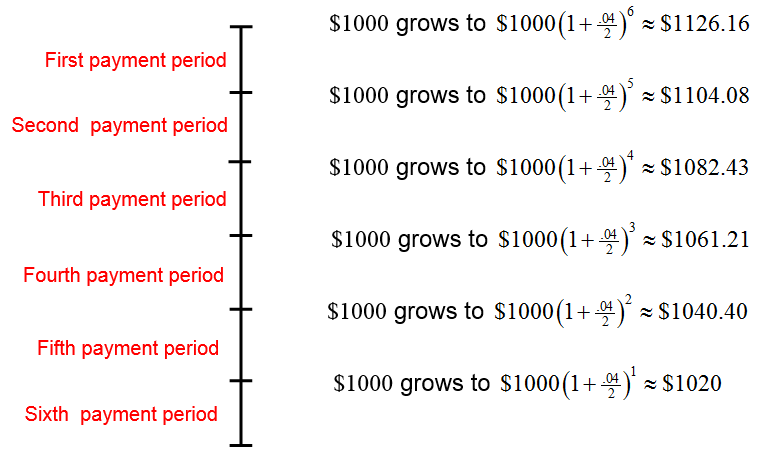
In an ordinary annuity, the payment into the annuity is made at the end of the period. An annuity due differs from this since the payments are made at the beginning of the period. However, we can apply the formula for determining the future value of an ordinary annuity with a little modification. Let’s look at the payments and the interest earned in an annuity due where payments of $1000 are made. As in our earlier example, these payments earn 4% interest compounded semiannually.
The sum of these payments and interest are
This sum contains the term 1000(1.02)6 corresponding to the amount the first payment grows to over six periods. Unlike the sum from a similar ordinary annuity, this sum does not contain a term equal to 1000. This is because the last payment is made at the beginning of the sixth payment period. It earns interest to grow to $1000(1.02) or $1020.
In effect, the future value of an annuity due is like an ordinary annuity with an extra period at the beginning of the annuity and lacking the final payment. This allows us to write the future value for the annuity due.
Future Value of an Annuity Due
If equal payments of PMT are made into an annuity due for n periods at an interest rate of i per period, the future value of the annuity FV is
This formula is almost identical to the future value of the ordinary annuity. The power of n+1 in the numerator incorporates the extra interest earned by the first payment. A payment is subtracted from the ordinary annuity formula to account for the last payment earning interest.
Example 5 Find the Future Value of an Annuity Due
An investor deposits $1000 in a simple annuity at the beginning of each six-month payment period. This annuity earns 4% per year, compounded semiannually. Find the future value if payments are made for three years.
Solution Since the payments are made at the beginning of each period, this is an annuity due. The payment is R = 500 and the interest rate per period is i = 0.05. Since interest is earned semiannually over the term of three years, there are n = 6 periods. Using these values, the future value is
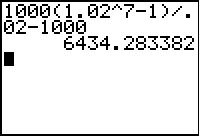
This is calculated on a TI Graphing Calculator as shown below.
This results in the same future value as adding the terms of the sum directly,