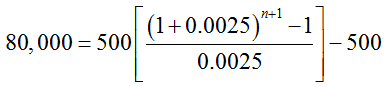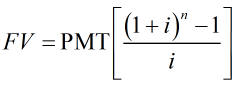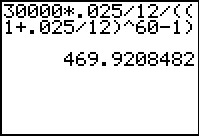What is a sinking fund?
If the future value of an annuity is fixed, the annuity is called a sinking fund. For instance, you anticipate that you will need $80,000 to fund you child’s education. If you set aside $500 each month in an interest bearing account to reach this goal, you have set up a sinking fund.
In problems involving sinking funds, the future value of the annuity is specified and some other quantity is determined. The formulas used depend on whether the payments are made at the beginning or end of each period.
Example 6 How Long Will It Take To Accumulate Some Amount?
The parents of a newborn child anticipate that they will need $80,000 for the child’s college education. They plan to deposit $500 in an account at the beginning of each month in an account that earns 3% interest compounded monthly. How long will it take them to reach their goal?
Solution This problem specifies a future value of $80,000. Since the payments are made at the beginning of each period, we’ll use the annuity due formula to calculate the length of time it will take to reach the future value.
The payment is R = 500 and the interest rate per period is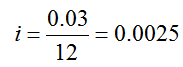 
When these values are put into the annuity due formula, we get
We need to solve this equation for the number of periods n. In doing this, we’ll avoid rounding any number. Rounding too early may lead to large changes in the value of n.
A period of approximately 135 months or a little over 11 years is needed to reach the goal. The number if periods is rounded up to insure the goal is reached. Rounding down would cause the accumulated amount to be slightly less than $80,000.
In some situations, we are interested in determining the payment that will yield a fixed future value.
Example 7 Find The Payment Needed To Accumulate a Fixed Amount
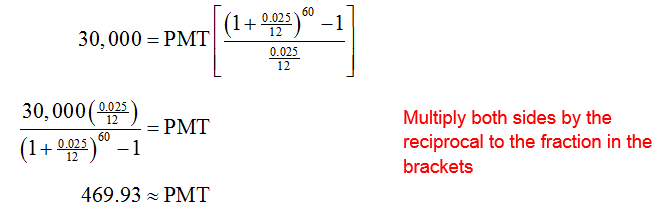
A new car buyer wishes to buy a vehicle with cash in five years. To do this, she wishes to deposit some amount at the end of each month in an account earning 2.5% interest compounded monthly. If she wishes to accumulate $30,000, what should the payments be?
Solution Since the payments are made at the end of each period, we’ll use the future value for an ordinary annuity,
to find the payment. Since the account has a balance of zero to begin with, the present value is zero. She wishes to accumulate $30,000, so FV = 30,000. Over five years, there are n = 12 · 5 or 60 periods with an interest rate per period of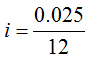 
. The value of this rate per period is not a terminating decimal so we will use the fraction throughout the calculation. Substitute the values into the formula above to give
This is calculated on a TI Graphing Calculator as shown below.
The payment is rounded up to insure the future value is reached. For this rounded payment, the future value will actually exceed 30,000 by about 58 cents. If the payments were rounded down, the future value would be slightly less than $30,000.