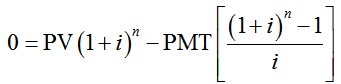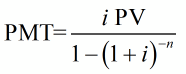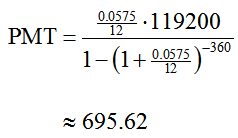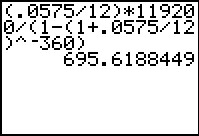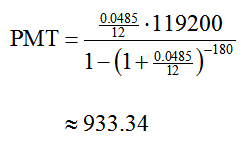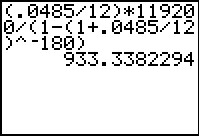How is a loan amortized?
Decreasing annuities may be used in auto or home loans. In these types of loans, some amount of money is borrowed. Fixed payments are made to pay off the loan as well as any accrued interest. This process is called amortization.
In the language of finance, a loan is said to be amortized if the amount of the loan and interest are paid using fixed regular payments. From the perspective of the lender, this type of loan is a decreasing annuity. The amount of the loan is the present value of the annuity. The payments from the annuity (to the lender) reduce the value of the annuity until the future value is zero.
This interpretation allows us to determine the payment PMT on a loan of PV dollars. Start with the decreasing annuity formula and set the future value FV equal to zero,
This equation is simplified to give
Now solve this equation for the payment PMT:
Payment on an Amortized Loan
Suppose a loan of PV dollars is amortized by periodic payments of PMT at the end of each period. If the loan has an interest rate of i per period over n periods, the payment is
We can use this formula to calculate the payment on any loan that is amortized. Pay special attention to the loan amount. Often the loan amount is not the same as the purchase price because of a down payment. A down payment is an amount paid up front that reduces the amount that must be borrowed. This amount must be subtracted from the purchase price to give the loan amount.
When a loan is amortized for the purchase of a home, the loan is called a mortgage. A typical mortgage is paid back over a 15 or 30 year period with monthly payments.
Example 3 Payment on an Amortized Loan
A young professor purchases a home for $149,000. He plans to take out a 30 year mortgage at an annual interest rate of 5.75%. The mortgage requires a down payment of 20% of the purchase price.
a. Find the monthly payment on this mortgage.
Solution To qualify for this loan, the professor must put 20% down,
Down Payment = 0.20 · 149,000 = 29,800
The loan amount is PV = 149,000 – 29,800 = 119,200. For a 30 year mortgage, there are n = 30 · 12 or 360 periods. The interest rate per period is i = 0.0575/12. Using these values, the monthly payment is
This calculation may be carried out on a TI graphing calculator as shown below.
This payment is usually rounded up to the nearest penny to insure the loan is paid off. In practice, this means the final payment will be slightly less than all other payments.
b. How much interest is paid on this mortgage?
Solution According to part a, the professor will pay a total of or $250,423.20 over the term of the loan. Since the loan amount is $119,200, the additional amount paid must be interest,
Interest = $250,423.20 – $119,200 = $131,223.20
The professor pays $131,223.20 in interest on this 30 year mortgage.
c. The professor has also discovered that he qualifies for a 15 year loan at an annual interest rate of 4.85%. This mortgage also requires a 20% down payment. Find the monthly payment on this mortgage.
Solution For this mortgage, the number of periods is n = 15 · 12 or 180. The intest rate per month is i = 0.0485/12. This leads to a payment of
The calculation is shown below on a TI Graphing Calculator.
Although the interest rate is lower for this mortgage, the shorter term leads to a higher monthly payment of $933.34.
d. How much interest is paid on the 15 year mortgage?
Solution The professor will pay a total of or $168,001.20 in payments. The interest is
Interest = $168,001.20 – $119,200 = $48,801.20
The professor pays $48,801.20 in interest on this 15 year mortgage.
Even though the 15 year mortgage has a lower interest rate, the shorter term leads to higher payments than the 30 year mortgage. However, because of the lower interest rate and shorter term, the amount of interest paid to the lender for the 15 year loan is almost a third of the interest paid on the 30 year loan. In general, loans with shorter terms have lower interest rates. This leads to less interest paid for shorter term loans.
The payments calculated above are the portion of a mortgage payment that applies to the loan. A typical mortgage payment also includes other amounts to cover property taxes, homeowners insurance, and mortgage insurance. These amounts can increase the overall payment by a large amount.