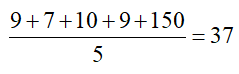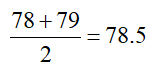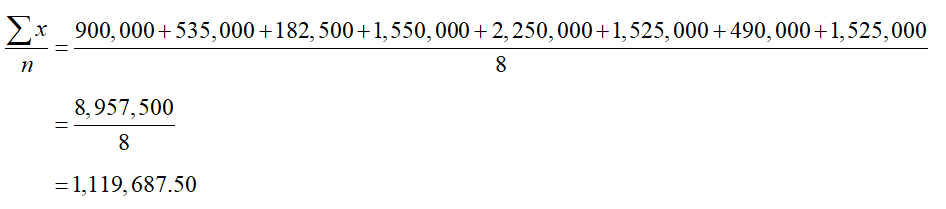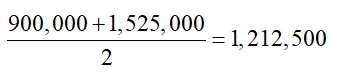What is the median of a dataset?
The mean has the disadvantage of being affected by extreme values in the data. For instance, suppose we find the mean of the data values 9, 7, 10, 9, and 15. Using the definition of the mean, we find
If we change the highest data value to an even higher value like 150, the mean increases significantly,
The median is a measure of central tendency that is not affected by extreme values (also called outliers) in the data.
Median
If the data is arranged in numerical order, the median is the center value that splits the data into two halves.
Once the data is arranged in numerical order, the center value may be determined by dividing the total number of data by 2. If the result is not an integer, round the quotient up to the nearest integer. The center value is located at this position when the data is listed in numerical order. If the quotient is an integer, the median is the mean of the data located in that position and the following position.
Example 4 Find the Median
Find the median of each set of data.
a. 9, 7, 10, 9, 15
Solution Start by arranging the data in numerical order.
7 9 9 10 15
There are five data values so the quotient for this dataset is 5/2 = 2.5. Rounding this value up to the nearest integer gives 3 indicating that the median is the third number when the data is written in numerical order. Since the third number is 9, the median is 9.
b. 49, 78, 92, 85, 79, 73
Solution Arrange the number is numerical order to give
49 73 78 79 85 92
This dataset has 6 values so 6/2 = 3. Since this number is an integer, the median is the mean of the values in the third and fourth positions in numerical order,
In part a of Example 5, the median was found to be 9. Notice that the median of a similar set of data containing an extreme value is the same. The median of the data 7, 9, 9, 10, 150 is also 9. This is due to the fact that swapping 15 for 150 does not change the center value. For this reason, the median is not affected by extreme values.
Example 5 Compare the Mean and Median
During the week of 6/7/2012 through 6/14/2012, eight homes were sold in Paradise Valley, Arizona in the area code 85253. The sales prices for these homes are listed below.
900,000 535,000 182,500 1,550,000 2,250,000 1,525,000 490,000 1,525,000
a. Find the mean sales price.
Solution Apply the definition of the mean to give
b. Find the median sales price.
Solution The selling prices in numerical order are
182,500 490,000 535,000 900,000 1,525,000 1,525,000 1,550,000 2,250,000
Since the dataset has 8 values, the median is the mean of the home sales at positions four and five,
c. Median sales prices are usually published instead of mean sales prices. Why is this a good idea?
Solution The mean is affected by extreme home sales. In this case, one of the home sales is 182,500 and is very low for this zip code. The low value drags the mean lower. In comparing the mean with the median, the mean is almost $100,000 lower because of this value. It is not desirable for an extreme home sale to affect the mean by so much so the median home sale is usually quoted instead of the mean home sale.