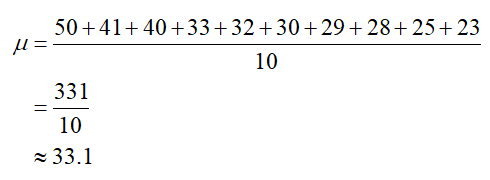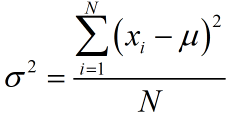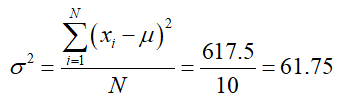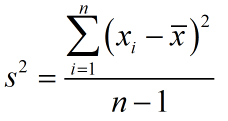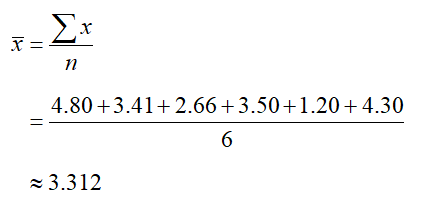What is the variance and standard deviation of a dataset?
The variance of the data uses all of the data to compute a measure of the spread in the data. The variance may be computed for a sample of data or a population of data. In either case, we must compute how much each data value differs from the mean and square that difference.
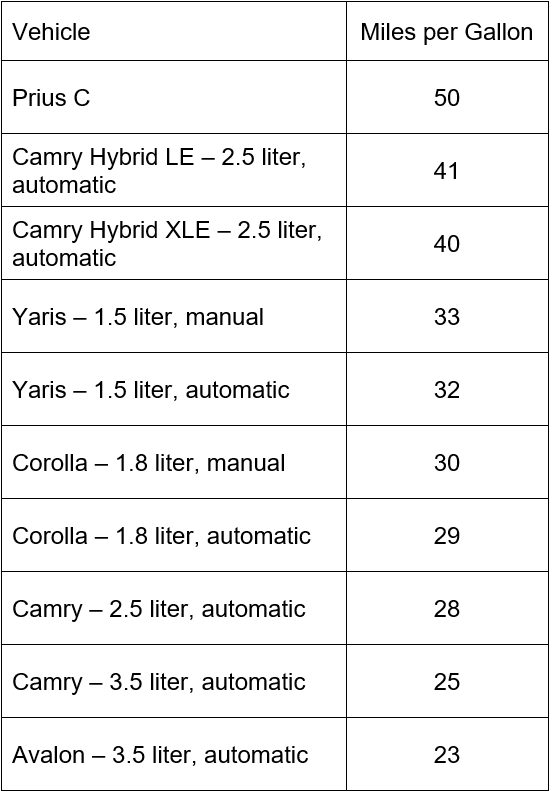
Let’s compute the variance for the mileage of Toyota sedans.
Start by computing the mean of this population,
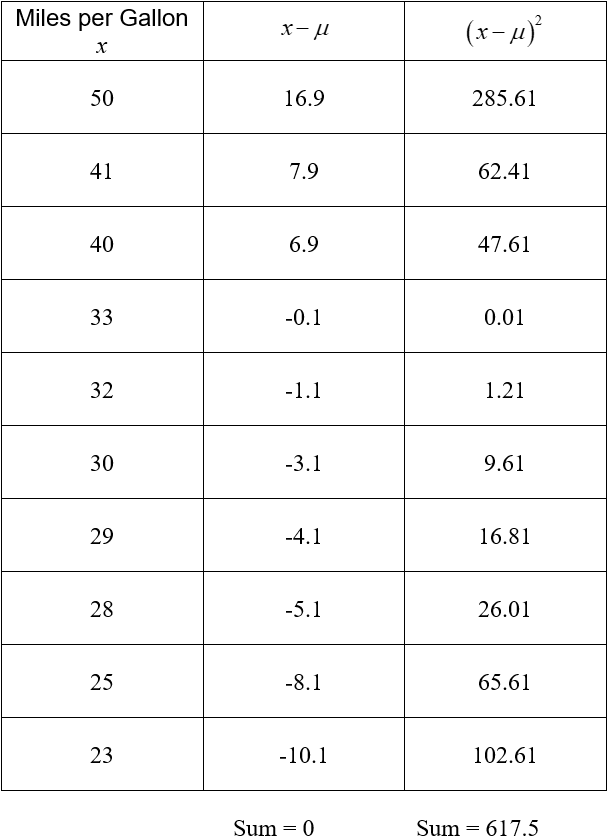
Next we subtract the mean from each data value and square the result.
The sum at the bottom is found by adding the values in the column. The second column measures how much each data value deviates from the mean. Values higher than the mean give a positive deviation and values lower than the mean give a negative deviation. Since the mean is in the center of the data, the sum of the deviations is zero.
Whether a data value falls above or below the mean should not affect the spread of the data. For this reason, each deviation is squared. The farther the data value is from the mean, the larger the squared deviation is. Values like 23 or 50 have a high squared deviation since they are farther from the mean of 33.1.
Population Variance
The population variance σ2 (sigma squared) of data is the mean of the squared deviations,
where μ is the population mean and N is the population size.
The variance measures the average amount the square of the distance each data value is from the mean. Based on the table above,
The sum in the numerator is the sum of the entries in the third column of the table. On average, each data values squared distance from the mean is 61.75 mpg2 from the mean.
Working in terms of the squared distance is inconvenient. To remedy this, take the square root of the variance. This measure is called the population standard deviation and measures the spread of the data in terms of the units on the data.
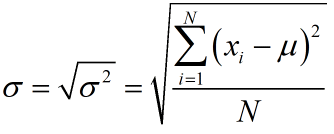
where μ is the population mean and N is the population size.
For the Toyota fleet, the standard deviation is
The larger the variance or standard deviation is, the more spread out the data values are about the mean.
If the data is from a sample instead of a population, the definitions for variance and standard deviation is slightly different.
Sample VarianceThe population variance s2 of data xi is the mean of the squared deviations,
where is the sample mean and n is the sample size.
Sample Standard Deviation
The sample standard deviation s is the square root of the sample variance,
The main difference between the sample and population standard deviation is the denominator. In the population expressions, the sum of the squared deviations from the mean is divided by the population size N. In the sample expressions, the sum of the squared deviations from the mean is divided by one less than the sample size n. Although the reason for this difference is beyond the scope of this text, using n – 1 instead of n insures that the variance is well behaved. Specifically, if we were to average all sample variances from a population, the resulting average is equal to the population variance.
Despite this difference, the steps for calculating variance and standard deviation for samples or populations is very similar.
- Identify the data values .
- Find the mean of the data values.
- Compute the difference between the data and the mean for each data value.
- Square each difference between the data and the mean.
- Sum the squares of the differences.
- If the data is a population, divide the sum by the number of data values N to find the variance. If the data is a sample, divide the sum by one less than the sample size, n – 1.
- To find the standard deviation, take the square root of the variance.
Let’s apply these steps to compute the spread in several datasets.
Example 1 Compute the Sample Variance and Sample Standard Deviation
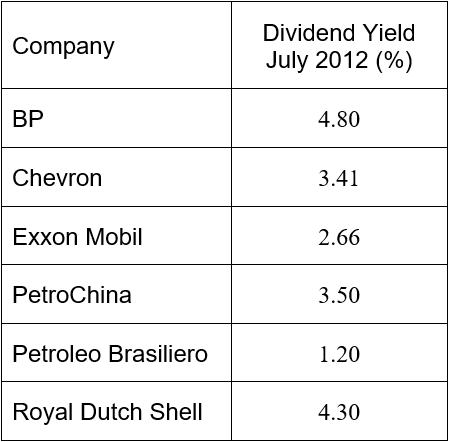
The table below shows the dividend yields of six companies in the New York Stock Exchange energy sector.
a. Find the sample mean.
Solution The data in this example are the dividend yields for each company. The sample mean is
The mean has been rounded to three decimal places.
b. Find the sample variance.
Solution Use a table to compute the differences from the mean and the squared differences from the mean.
Divide the sum at the bottom of the third column by 5 to give the sample variance,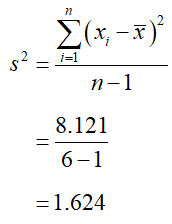
c. Find the sample standard deviation.
Solution The sample standard deviation is the square root of the sample variance,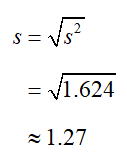
In this example, the original data was written to two decimal places. To insure that we can write the standard deviation to the same number of decimal places, we write numbers in the intermediate steps to one extra decimal place.
Example 2 Compute the Population Variance and Population Standard Deviation
Stock quotes also give the percentage change in a stock from the previous day’s closing price.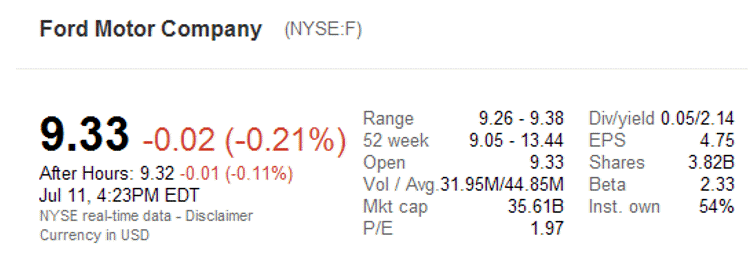
For instance, the quote above indicates that Ford closed at $9.33 per share. This was down from $9.31 per share on the previous days close. This is a percentage change of
Percentage changes are often used to determine the volatility of a company’s stock. By computing some statistics on the percentage change, we can get an idea whether a change in the price is normal or not. Consider the percentage changes in Ford’s price per share over ten trading days in June.
a. Find the population mean.
Solution For the purpose of this example, we’ll consider the percentage changes over the ten day period to be a population. The mean is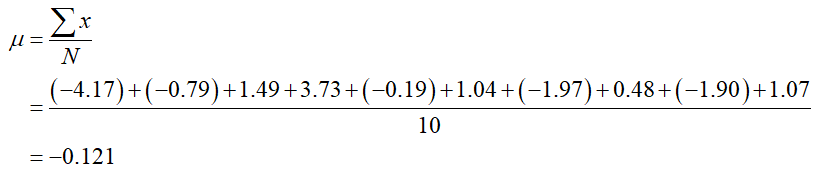
b. Find the population variance.
Solution Calculate the difference from the mean and the squared difference from the mean.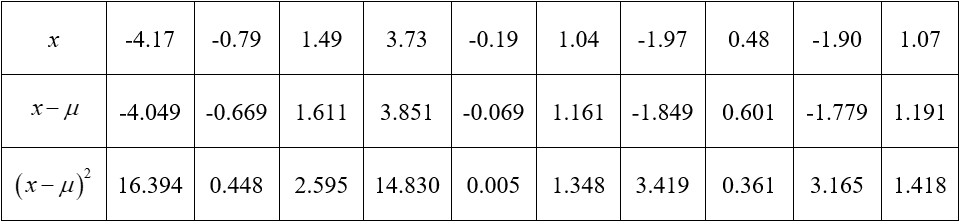
The sum of the bottom row is 43.983. The population variance is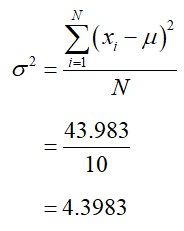
c. Find the population standard deviation.
Solution The standard deviation is the square root of the variance,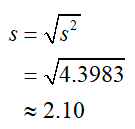
We’ll see in later chapters that stock traders assume that 68% of stock changes lie within one standard deviation of the mean. A change in price of greater that 2.10% indicates above normal strength or weakness, depending on whether the price rises or falls.