Students are often surprised when they graph a parabola a notice that the parabola has no x intercepts.
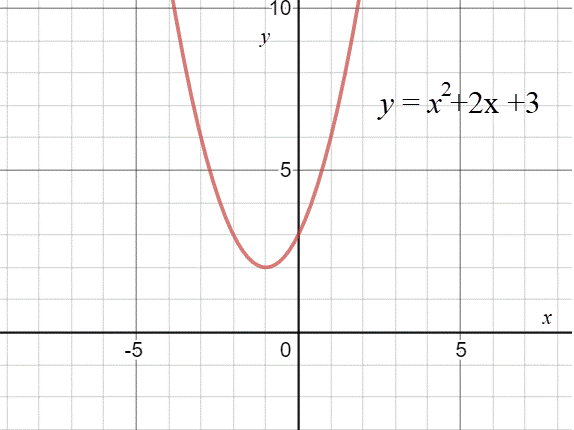
But as the graph above shows, parabolas do exist that do not cross the x axis.
However, suppose you do not have the graph of y = x2 +2x+3 available. How could you use the equation to determine whether this parabola has any x intercepts?
Let’s start by following the usual process for finding x intercepts of any graph. Set y = 0 to get the equation
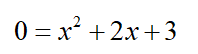
This is a quadratic equation with a = 1, b = 2, and c = 3. To solve this equation, we need to use the quadratic formula:
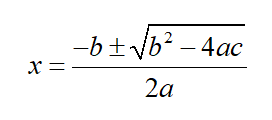
Now put in the values for a, b, and c. This gives us
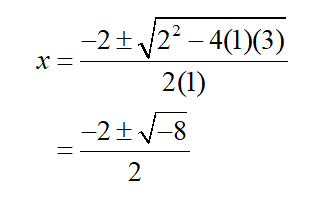
This might set off alarms in your mathematical brain!
How can you take the square root of a negative number? For numbers graphed on a real number graph, you can’t. That is why our graph above has no x intercepts. However, if we expand our knowledge of numbers to complex numbers, we can write out a solution to the quadratic equation 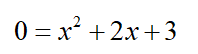
In complex numbers, 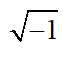
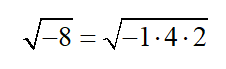
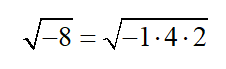
Since i = 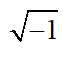
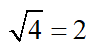
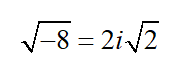
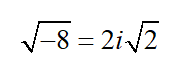
And our solution to the quadratic equation as
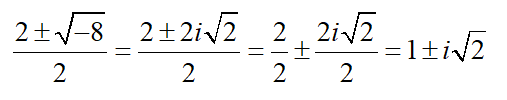
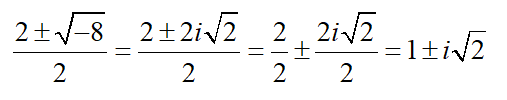
In short, the quadratic equation has a solution that uses i. Since our graph does not allow for this type of number, it shows no x intercepts.
