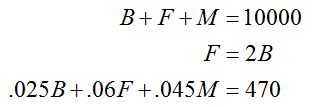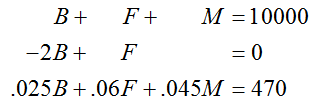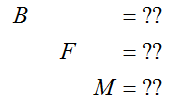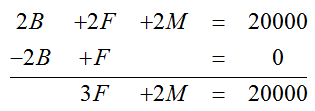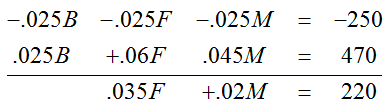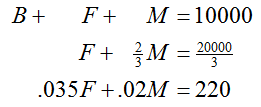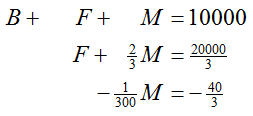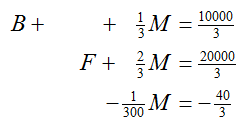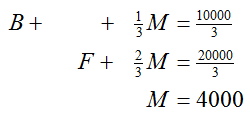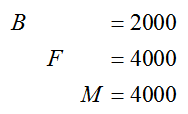The most common mistakes in solving problems with systems of linear equations is in setting up the problem in the first place. In the example below, note how the variables are defined carefully so that the difference between amounts of money invested is distinguished from amounts of interest.
Example Katherine Chong invests 10,000 dollars received from her grandmother in three ways. With one part, she buys US savings bonds at an interest rate of 2.5% per year. She uses the second part, which amounts to twice the first, to buy mutual funds that offer a return of 6% per year. She puts the rest of the money into a money market account paying 4.5% annual interest. The first year her investments bring a return of 470 dollars. How much did she invest in each way?
Write Out The Equations
For any problem like this, we want to determine what the variables are and what they represent. Since the question asks, “How much did she invest in each way?”, let’s define
B: amount invested in bonds
F: amount invested in mutual funds
M: amount invested in money market account
How do these amounts relate to the other key totals given in the problem?
A total of 10,000 dollars invested.
The amount of invested in mutual funds is twice that invested in savings bonds.
The total return from the investments is 470 dollars.
We need to use the three facts to write out three equations in the three variables. Let’s look at each of the three facts.
A total of $10,000 invested
Since the variables represent the amounts invested, this statement simply says that the sum of the variables is 10,000 or
B + F + M = 10000
This type of fact is usually the easiest to write as an equation.
The amount of invested in mutual funds is twice that invested in savings bonds
Let’s identify the variables in this statement:
If we now translate this to a mathematical equation, we get
F = 2B
The total return from the investments is $740
To calculate the return on an investment, we need to multiply the percent return as a decimal times the amount invested at that percent. For instance, if B dollars are invested in bonds returning 2.5% per year then the amount returned from that investment in a year is .025 B. If we apply this thinking to each investment, we get that
.025B + .06F + .045M = 470
Now that we have three equations in three unknowns, let’s write out the system:
Rewrite the second equation by subtracting 2B from both sides:
Solve for Variables
We solve this system so that it looks like
where ?? are different numbers. To put in this form, we’ll utilize row operations. We’ll begin by making sure the coefficient on B in the first equation is a 1. Since it is, we do not need to use a row operation to make it so.
Now we’ll eliminate B from the second and third equations using the first equation. Use the operations
2E1 + E2 → E2
-.025E1 + E3 → E3
Let’s examine the first carefully:
Now the second operation
Writing out the operations makes them easier to check later on. Rewriting the system after these operations leaves us with
Notice that the first equation has a 1 in front of the first variable and the same variable has been eliminated from the other equations.
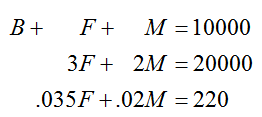
Now let’s make the coefficient on the second variable in the second equation equal to 1 using ⅓E2 → E2. The system is now
To eliminate F from the third equation, carry out -.035E2 + E3 → E3. Carrying out this operation gives us
Now let’s eliminate F from the first equation with -1E2 + E1 → E1 . Now the system is
Notice that these last few steps put a 1 in front of the second variable in the second equation and eliminate F in the other equations.
The last step in putting the system in echelon form is to make the coefficient on the third variable in the third equation a 1. To do this, -300E3 → E3. After multiplying the last equation, we have
Now let’s eliminate M from the first and second equation,
-⅔E3 + E2 → E2
-⅓E3 + E1 → E1
This gives
This means $2000 must be invested in bonds, $4000 in mutual funds, and $4000 in the money market account. As it should, the amounts add to $10,000 and there is twice as much in mutual funds as bonds. The total annual return is
The solution meets all of the requirements of the problem so it must be correct (unless we misinterpreted those requirements).
Note that we could solve the original system with matrices also and end up with the same solution.
What if the problem had said something like
The return on mutual funds is twice the return on savings bonds.
instead of
The amount of invested in mutual funds is twice that invested in savings bonds
Our problem above dealt with amounts invested…this new wording indicates a relationship between the returns. The rate on mutual funds is 6% so the return would be .06F. THe rate on bonds is 2.5% so the return would be .025B. Then this information is written in equation form as
.06F = 2 (.025B)
In this case, this would replace the second equation in the system.