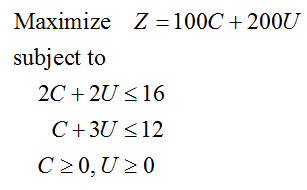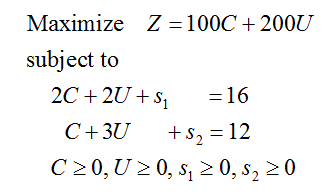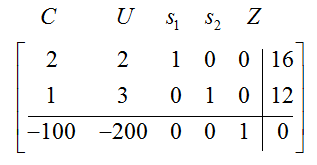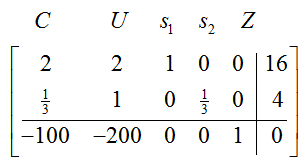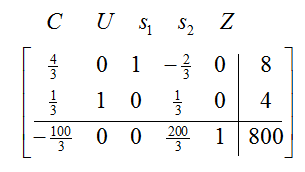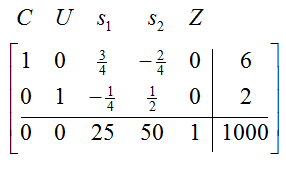Carrie Green is working to raise money for the homeless by sending information letters and making follow up calls to local labor organizations and church groups. She discovers that each church group requires 2 hours of letter writing and 1 hour of follow up while for each labor union she needs 2 hours of letter writing and 3 hours of follow up. Carrie can raise 100 dollars from each church group and 200 dollars from each union local, and she has a maximum of 16 hours of letter writing time and a maximum of 12 hours of follow up time available per month. Determine the most profitable mixture of groups she should contact and the most money she can raise.
Set Up The Linear Programming Problem
To get started, we need to identify the variables in this problem. Since the problem asks us to “determine the most profitable mixture of groups she should contact”, let’s define
C: number of church groups to contact
U: number of union locals to contact
With these two variables defined, let’s find the objective function. The problem statement asks us to determine “the most money she can raise”. Since she can raise 100 dollars from each church group and 200 dollars from each union local, the objective function must be
Z = 100C + 200U
Now look for the factors that constrain her fundraising. Two pieces of information are evident:
she has a maximum of 16 hours of letter writing time
she has a maximum of 12 hours of follow up time
This leads me to write
Let’s tackle the first piece of information. Since it regards letter writing, let’s find the information for letter writing.
each church group requires 2 hours of letter writing
each labor union she needs 2 hours of letter writing
So if we have C church groups and U union locals, we can write
2C + 2U ≤ 16
Following a similar strategy for follow up leads us to
C + 3U ≤ 12
Now that we have the objective function and the constraints, we can write out the linear programming problem:
Now we can carry out the simplex method.
Carry Out The Simplex Method
Rewrite the problem with two slack variables:
The initial tableau is
The pivot column is the second column since -200 is the most negative entry in the indicator row. The pivot row is the second row since 12/3 < 16/2. Therefore we need to change the 3 in the pivot entry to a 1 by performing 1/3 R2 → R2:
Now we need to put 0’s in the rest of the pivot column by performing -2 R2 + R1 → R1 and 200 R2 + R3 → R3:
Since there is a negative number in the indicator row, we need to pivot again. The new pivot is the 4/3 in the first row, first column. We begin by changing the pivot to a 1 by performing 3/4 R1 → R1:
To put 0’s in the rest of the column, perform –1/3 R1 + R2 → R2 and 100/3 R1 + R3 → R3:
Since there are no negative numbers in the indicator row, we have arrived at the maximum amount of money raised, $1000. This is done by contacting 6 church groups and 2 union locals.