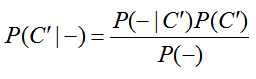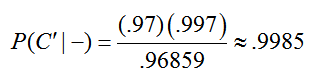The probability of colorectal cancer can be given as .3%. If a person has colorectal cancer, the probability that the hemoccult test is positive is 50%. If a person does not have colorectal cancer, the probability that he still tests positive is 3%.
What is the probability that a person who tests negative does not have colorectal cancer?
To solve this problem, we’ll draw and label an appropriate tree diagram. Then we’ll apply Bayes’ Rule to the problem. Look at the information given in the problem. If
C is the event “person has colorectal cancer”
+ is the event “the hemoccult test is positive”
– is the event “the hemoccult test is negative”
we know that
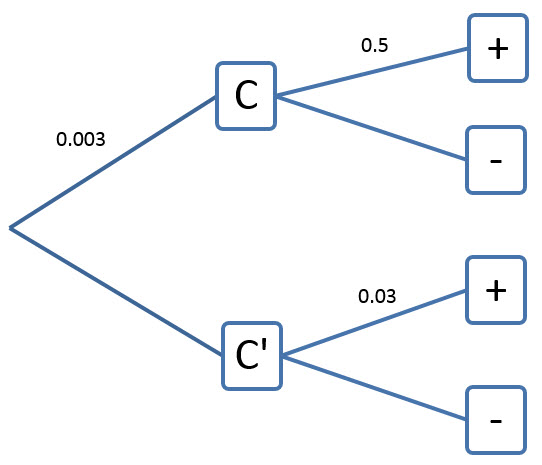
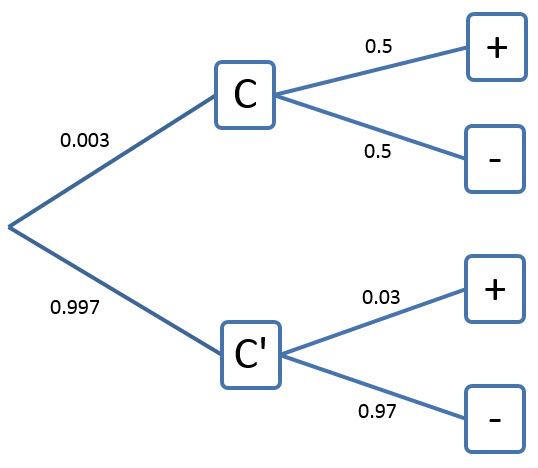
P(C) = 0.003
P(+ | C) = 0.5
P(+ | C ′ ) = 0.03
This suggests the following tree diagram:
Knowing that the sum of the probabilities from one point on the tree should add to 1, we can finish the tree diagram as follows:
The probability we are looking for is P(C ′ | -). Notice that the tree diagram has P(- | C ′ ), but not the reverse conditional probability that we are looking for. This is a sign we need to use Bayes’ Rule. Let’s find the appropriate form of Bayes’ Rule. The relationship between the conditional probabilities is
Solving for P(C ′ | -) gives
This is Bayes’ Rule for this problem. Now we are ready to use the tree diagram. P(- | C ′ ) and P(C ′ ) are both labeled on the tree diagram. We can calculate P(-) by following the branches on the tree diagram (multiply) that lead to a negative result, and then summing up the products from these branches.
Putting these values into Bayes’ Rule gives
This means that is you test negative, the likelihood that you do not have colorectal cancer is 99.85%. The test is quite good at screening that you do not have the disease.