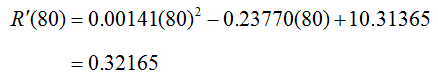In many business problems, we are interested in knowing the rate at which some quantity is changing. If this quantity is modeled by a function, the rate is modeled by the derivative of the function.
In the problem below, we are given a model of revenue for Verizon, a national wireless carrier. To find the rate, we’ll need to take the derivative of the revenue function.
From 2006 through 2011, Verizon Wireless grew steadily. As the number of connections increased, so did the revenue from those connections.A cubic model for the revenue over this period is
where c is the number of connections in millions.
At what rate is the revenue increasing when there are 80,000,000 connections?
Questions that ask about rate or refer to “marginal” are questions about the derivative. In this case, it is referring to the value of the derivative at c = 80. The derivative of the revenue function is
The value of the derivative at 80 million connections is
To find the units on this rate, recall that the derivative is also the slope of the tangent line at c = 80. The slope of this line has vertical units of billions of dollars and horizontal units of millions of connections. This may be simplified to
Since a billion divided by a million is one thousand. So means that an additional connection at this level results in an increase in revenue of 0.31265 thouusand dollars or $321.65.