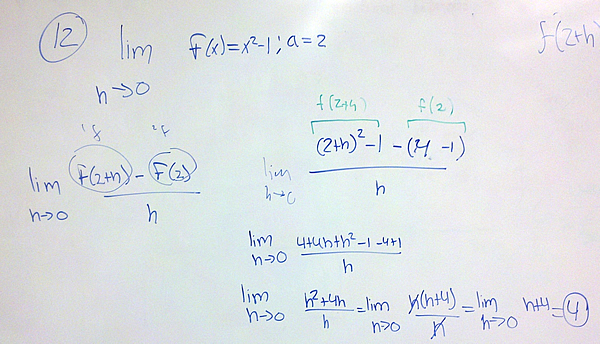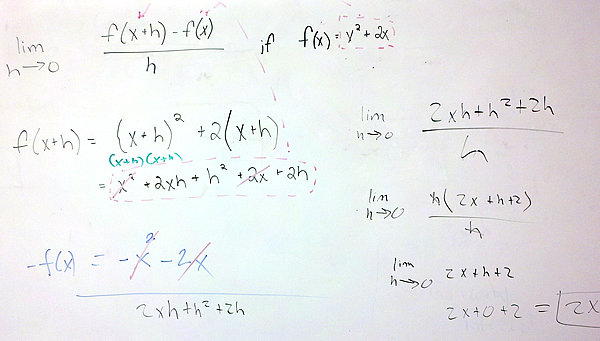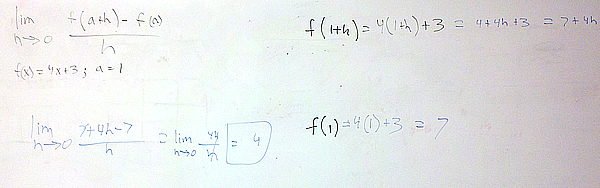The last part of Section 10.3 asks you to compute several different difference quotients. Some of the problems ask you to compute
$latex \underset{h \to 0}{\mathop{lim }},\frac{f(a+h)-f(a)}{h}$
where f(x) and a are given to you in the problem. Here are a few examples from the board.
$latex f(x)=4x+3$ and $latex a=1$
The board above contains a mistake…do you see where this group made a mistake?
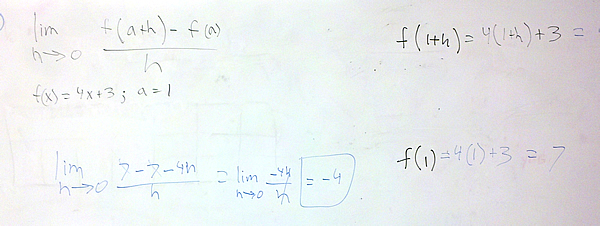
$latex f(x)={{x}^{2}}-4$ and $latex a=1$
$latex f(x)={{x}^{2}}-1$ and $latex a=2$
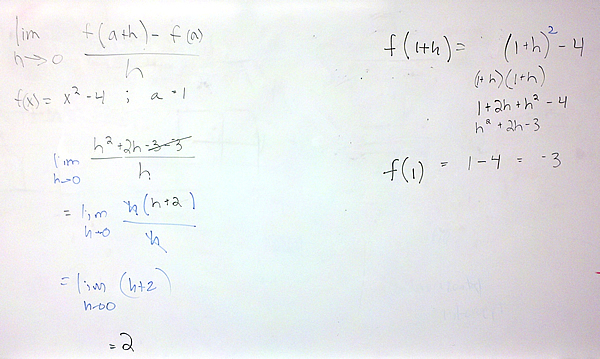
In the examples below, you are asked to compute a difference quotient containing x instead of a.
Compute $latex \underset{h \to 0}{\mathop{lim }},\frac{f(x+h)-f(x)}{h}$ where $latex f(x)={{x}^{2}}+2x$
Compute $latex \underset{h \to 0}{\mathop{lim }},\frac{f(x+h)-f(x)}{h}$ where $latex f(x)={{x}^{2}}-x$
By the way, the correct solution to the first problem is below.
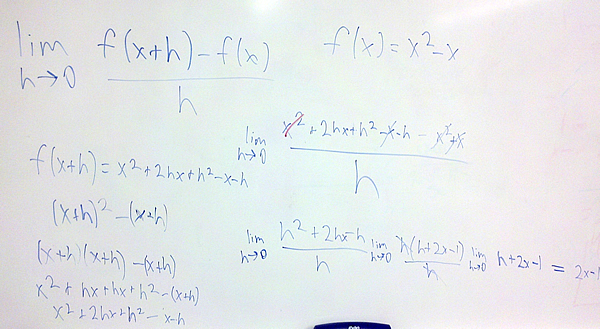
In this original calculation, f(a+h) and f(a) where switched.