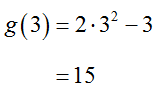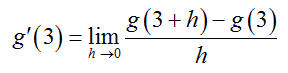
Problem Suppose the function g(x) is given by
Use the definition of the derivative at a point to compute g´(3).
Solution The definition of the derivative of g(x) at x = 3 is
The function value g(3) is calculated to be
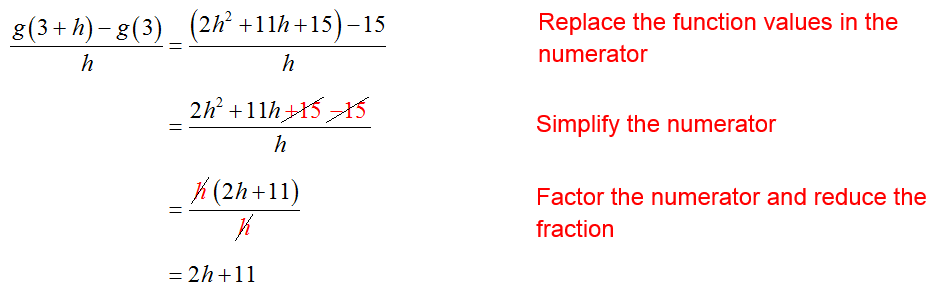
The function value g(3 + h) must be calculated carefully.
Form the difference quotient and simplify:
The derivative is completed by taking the limit as h approaches zero,
The derivative of g(x) evaluated at x = 3, g´(3), is 11.