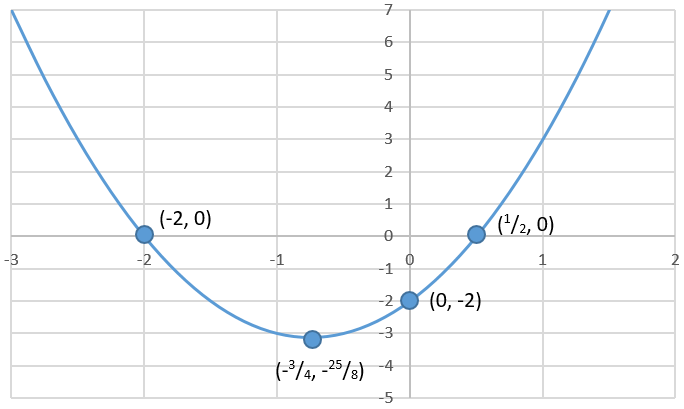
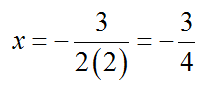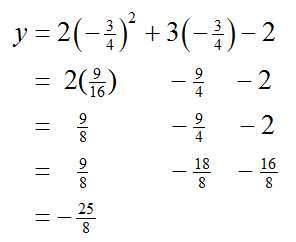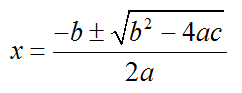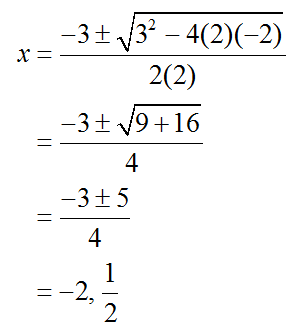Let’s look at how to use formulas for a parabola to get certain important points on a parabola.
Problem For the parabola y = 2x2 + 3x – 2, locate the points below.
a. The y-intercept.
Solution At the y-intercept, the x value is zero. This means that we need to set x = 0 in the equation:
y = 2(02) + 3(0) – 2 = -2
Putting this together, the y-intercept is at (0, -2).
b. The vertex.
Solution The vertex is located using the formula 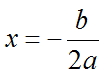
To find the corresponding y value, put this value into the equation,
This means the vertex is at (-3/4, –25/8).
c. The x-intercepts.
Solution At the x-intercepts, the y value is zero. Putting this into the equation yields
0 = 2x2 + 3x – 2
This equation is solved with the quadratic formula,
Put the values from the equation (a = 2, b = 3, and c = -2),
The x intercepts are at (-2, 0) and (1/2, 0).
All of these points are shown in the graph of the parabola below.