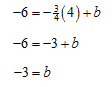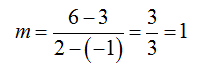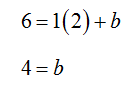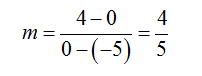In this FAQ, I’ll demonstrate how we can use y = mx + b to find equations of lines. No need to memorize other equations of lines…it is easier to focus on the data given to us an use it to find m and b.
Let’s look at the most basic example that illustrates this process.
a. Find the equation of a line through the point (4, -6) with slope – 3/4.
Start by substituting m = -3/4 in the slope-intercept form to yield
y = – 3/4 x + b
Now substitute the point into the line by setting x = 4 and y = -6. This leads to
Using this value for b in the slope-intercept form above give the line y = –3/4 x -3. The answer to the problem is the equation of the line with the appropriate values for m and b.
Now let’s complicate matters a bit by finding the equation of a line passing through two points.
b. Find a line through the points (-1, 3) and (2, 6).
The slope through the points is
Substitute the slope into the slope-intercept form to give
y = x + b
Now take one of the points and substitute it into this equation. Using the ordered pair (2, 6), we can solve for b:
This gives us the equation y = x + 4.
In both of these examples we applied the same strategy of putting in the slope m and then solving for the intercept b.
Now let’s look at a problem whose wording might throw you off.
c. Find a line with x-intercept of -5 and a y-intercept of 4.
Don’t let the fact that they talk about intercepts throw you off the strategy. These intercepts can be written as ordered pairs (-5, 0) and (0, 4). The slope between these points is
This leads to the line
y = 4/5 x + b
Since the y-intercept is 4, we can substitute it into this line for b to give y = 4/5 x + 4 .
This problem is even easier since the y intercept was given to us. In each case we can start from y = mx + b and then find the value of m and b.