Equilibrium points are easy to find when the supply and demand functions are given by formulas….just set the formulas equal to each other to find the point of intersection. But what about when the supply and demand are data? The example below shows how to get the formulas for each function and then to find the equilibrium point.
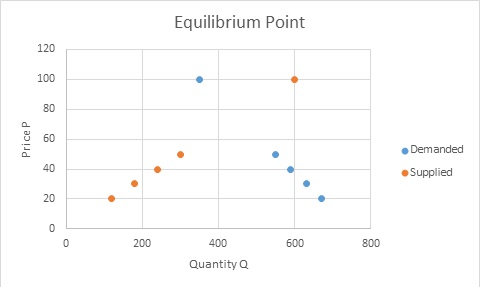
The table below gives the quantity of boojuminators demanded and the quantity supplied for selected prices.
|
Price ($) |
Quantity Demanded (thousands) |
Quantity Supplied (thousands) |
|
20 |
670 |
120 |
|
30 |
630 |
180 |
|
40 |
590 |
240 |
|
50 |
550 |
300 |
|
100 |
350 |
600 |
a. Find the price demand and price supply as a function of the quantity Q.
Let’s start by graphing the data. Since we want each function written as a function of Q, graph the quantity Q horizontally and the price P vertically. This means each point is of the form (Q, P).
Each function appears to be linear so they may be written in the form
$latex \displaystyle P=mQ+b$
The slope of the demand function is
$latex \displaystyle {{m}_{d}}=\frac{30-20}{630-670}=-\frac{1}{4}$
This function must pass through one of the points like (670, 20) so we can solve for b:
$latex \displaystyle 20=-\frac{1}{4}\left( 670 \right)+b$
$latex \displaystyle 187.5=b$
This means the demand function is
$latex \displaystyle P=-\frac{1}{4}Q+187.5$
The slope of the supply function is
$latex \displaystyle {{m}_{s}}=\frac{30-20}{180-120}=\frac{1}{6}$
Using the point (120, 20) we can solve for b on the supply function:
$latex \displaystyle 20=\frac{1}{6}\left( 120 \right)+b$
$latex \displaystyle 0=b$
The supply function is
$latex \displaystyle P=\frac{1}{6}Q$
b. Find the equilibrium point.
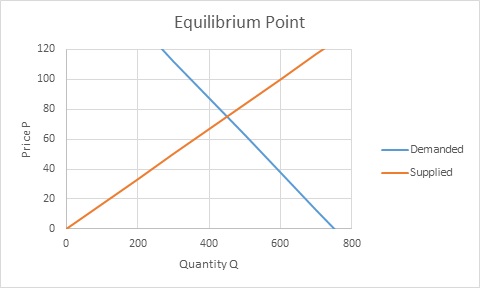
We graph these functions to show the point of intersection which is the equilibrium point.
Solve the system
$latex \displaystyle P=-\frac{1}{4}Q+187.5$
$latex \displaystyle P=\frac{1}{6}Q$
by substitution to give
$latex \displaystyle \frac{1}{6}Q=-\frac{1}{4}Q+187.5$
Multiply both sides of the equation by 24 to remove the fractions,
$latex \displaystyle 24\left( \frac{1}{6}Q \right)=24\left( -\frac{1}{4}Q \right)+24\left( 187.5 \right)$
$latex \displaystyle 4Q=-6Q+4500$
$latex \displaystyle 10Q=4500$
$latex \displaystyle Q=450$
The corresponding price is
$latex \displaystyle P=\frac{1}{6}\left( 450 \right)=75$